2025-09-28：使 K 个子数组内元素相等的最少操作数。用go语言，给定一个整数数组 nums 和两个整数 x、k。

你可以对数组中的任意元素做任意次“加一或减一”的单位操作（也可以不做任何操作）。

任务是通过尽可能少的这类操作，让数组里出现至少 k 段长度正好为 x、且互不重叠的连续区间——每一段内的所有数都相等（不同段之间的值可以一样也可以不同）。

其中“子数组”指的是数组中的连续一段元素。

返回达到该目标所需的最小操作次数。

2 <= nums.length <= 100000。

-1000000 <= nums[i] <= 1000000。

2 <= x <= nums.length。

1 <= k <= 15。

2 <= k * x <= nums.length。

输入： nums = [5,-2,1,3,7,3,6,4,-1], x = 3, k = 2。

输出： 8。

解释：

进行 3 次操作，将 nums[1] 加 3；进行 2 次操作，将 nums[3] 减 2。得到的数组为 [5, 1, 1, 1, 7, 3, 6, 4, -1]。

进行 1 次操作，将 nums[5] 加 1；进行 2 次操作，将 nums[6] 减 2。得到的数组为 [5, 1, 1, 1, 7, 4, 4, 4, -1]。

目前，子数组 [1, 1, 1]（下标 1 到 3）和 [4, 4, 4]（下标 5 到 7）中的所有元素都相等。总共进行了 8 次操作，因此输出为 8。

题目来自力扣3505。

解决步骤

步骤1：预计算所有长度为x的子数组的”到中位数的距离和”

这是整个算法的关键预处理步骤：

1. 使用双堆维护滑动窗口的中位数：

• 维护一个最大堆 left（存储较小的一半元素）和一个最小堆 right（存储较大的一半元素）

• 保持 left 的大小等于或比 right 多1，这样中位数就是 left 的最大值

2. 计算距离和的高效方法：

• 设中位数为 m

• 左半部分元素的和：s1 = m * left.size – left.sum（由于left中存储的是取反后的值）

• 右半部分元素的和：s2 = right.sum – m * right.size

• 总操作数 = s1 + s2

3. 懒删除优化：

• 使用 lazyHeap 结构记录需要删除但尚未实际删除的元素

• 只有在访问堆顶时才执行实际的删除操作

这一步为每个可能的起始位置 l 计算了将 nums[l:l+x] 变为一样值的最小操作数，存储在 dis 数组中。

步骤2：动态规划选择最优的k个子数组

目前问题转化为：从 dis 数组中选择 k 个互不重叠的区间（每个区间长度为 x），使得总操作数最小。

1. 状态定义：

• 使用滚动数组 f 和 g 来节省空间

• f[j] 表明思考前 j 个位置时，选择若干个子数组的最小总操作数

2. 状态转移：

• 对于第 i 个子数组（i 从 1 到 k）

• 遍历可能的结束位置 j（从 i*x 到 n-(k-i)*x）

• 状态转移方程：g[j] = min(g[j-1], f[j-x] + dis[j-x])

• 其中 dis[j-x] 表明以 j-x 为起点的子数组的操作代价

3. 边界条件处理：

• 确保子数组之间不重叠（间隔至少为 x）

• 确保剩余空间足够放置剩余的子数组

步骤3：返回结果

最终的答案就是 f[n]，即思考整个数组时选择 k 个子数组的最小总操作数。

具体示例分析

对于输入 nums = [5,-2,1,3,7,3,6,4,-1], x = 3, k = 2：

1. 预计算所有长度为3的子数组的代价：

• 子数组1: [5,-2,1] → 中位数1，代价 = |5-1| + |-2-1| + |1-1| = 4+3+0 = 7

• 子数组2: [-2,1,3] → 中位数1，代价 = 3+0+2 = 5

• …以此类推

2. 动态规划选择2个不重叠的子数组，找到最小总代价为8：

• 选择子数组 [1,3,7]（索引2-4）和 [3,6,4]（索引5-7）

• 或者选择其他组合，但总代价最小为8

复杂度分析

时间复杂度

• 预计算阶段：使用双堆维护滑动窗口的中位数，每个元素入堆出堆一次，时间复杂度为 O(n log n)

• 动态规划阶段：状态数为 O(nk)，每个状态转移是 O(1)，时间复杂度为 O(nk)

• 总时间复杂度：O(n log n + nk)

空间复杂度

• 预计算阶段：双堆和懒删除映射需要 O(n) 空间

• 动态规划阶段：使用滚动数组，只需要 O(n) 空间

• 总空间复杂度：O(n)

其中 n 是数组长度，k 是子数组个数（k ≤ 15），x 是子数组长度。

Go完整代码如下：

package main

import (
    "container/heap"
    "fmt"
    "math"
    "sort"
)

// 480. 滑动窗口中位数（有改动）
// 返回 nums 的所有长为 k 的子数组的（到子数组中位数的）距离和
func medianSlidingWindow(nums []int, k int) []int {
    ans := make([]int, len(nums)-k+1)
    left := newLazyHeap()  // 最大堆（元素取反）
    right := newLazyHeap() // 最小堆

    for i, in := range nums {
        // 1. 进入窗口
        if left.size == right.size {
            left.push(-right.pushPop(in))
        } else {
            right.push(-left.pushPop(-in))
        }

        l := i + 1 - k
        if l < 0 { // 窗口大小不足 k
            continue
        }

        // 2. 计算答案
        v := -left.top()
        s1 := v*left.size + left.sum // sum 取反
        s2 := right.sum - v*right.size
        ans[l] = s1 + s2

        // 3. 离开窗口
        out := nums[l]
        if out <= -left.top() {
            left.remove(-out)
            if left.size < right.size {
                left.push(-right.pop()) // 平衡两个堆的大小
            }
        } else {
            right.remove(out)
            if left.size > right.size+1 {
                right.push(-left.pop()) // 平衡两个堆的大小
            }
        }
    }

    return ans
}

func newLazyHeap() *lazyHeap {
    return &lazyHeap{removeCnt: map[int]int{}}
}

// 懒删除堆
type lazyHeap struct {
    sort.IntSlice
    removeCnt map[int]int// 每个元素剩余需要删除的次数
    size      int         // 实际大小
    sum       int         // 堆中元素总和
}

// 必须实现的两个接口
func (h *lazyHeap) Push(v any) { h.IntSlice = append(h.IntSlice, v.(int)) }
func (h *lazyHeap) Pop() any   { a := h.IntSlice; v := a[len(a)-1]; h.IntSlice = a[:len(a)-1]; return v }

// 删除
func (h *lazyHeap) remove(v int) {
    h.removeCnt[v]++ // 懒删除
    h.size--
    h.sum -= v
}

// 正式执行删除操作
func (h *lazyHeap) applyRemove() {
    for h.removeCnt[h.IntSlice[0]] > 0 {
        h.removeCnt[h.IntSlice[0]]--
        heap.Pop(h)
    }
}

// 查看堆顶
func (h *lazyHeap) top() int {
    h.applyRemove()
    return h.IntSlice[0]
}

// 出堆
func (h *lazyHeap) pop() int {
    h.applyRemove()
    h.size--
    h.sum -= h.IntSlice[0]
    return heap.Pop(h).(int)
}

// 入堆
func (h *lazyHeap) push(v int) {
    if h.removeCnt[v] > 0 {
        h.removeCnt[v]-- // 抵消之前的删除
    } else {
        heap.Push(h, v)
    }
    h.size++
    h.sum += v
}

// push(v) 然后 pop()
func (h *lazyHeap) pushPop(v int) int {
    if h.size > 0 && v > h.top() { // 最小堆，v 比堆顶大就替换堆顶
        h.sum += v - h.IntSlice[0]
        v, h.IntSlice[0] = h.IntSlice[0], v
        heap.Fix(h, 0)
    }
    return v
}

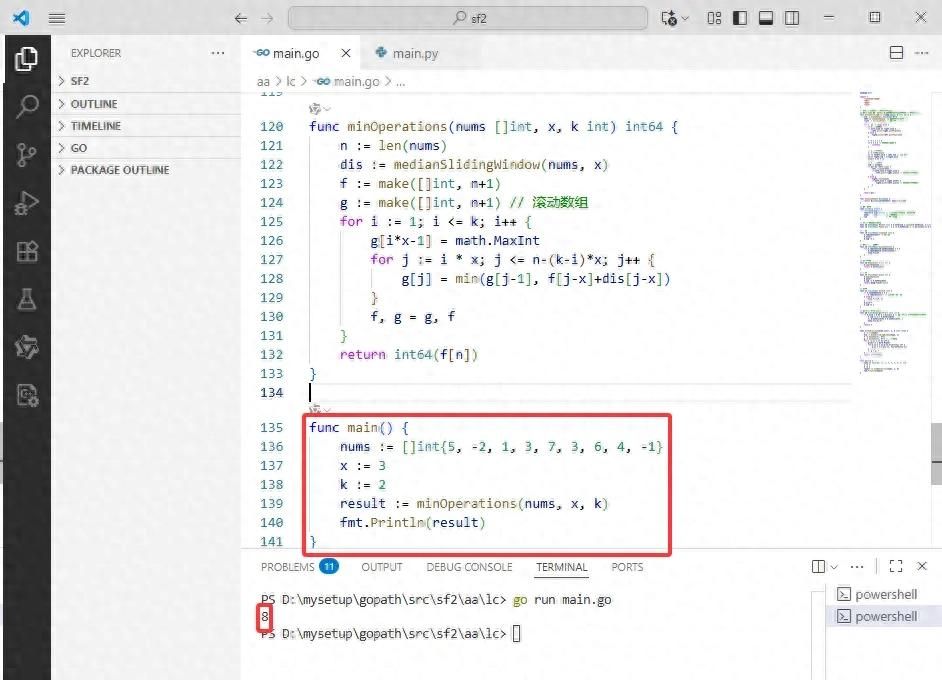
func minOperations(nums []int, x, k int)int64 {
    n := len(nums)
    dis := medianSlidingWindow(nums, x)
    f := make([]int, n+1)
    g := make([]int, n+1) // 滚动数组
    for i := 1; i <= k; i++ {
        g[i*x-1] = math.MaxInt
        for j := i * x; j <= n-(k-i)*x; j++ {
            g[j] = min(g[j-1], f[j-x]+dis[j-x])
        }
        f, g = g, f
    }
    returnint64(f[n])
}

func main() {
    nums := []int{5, -2, 1, 3, 7, 3, 6, 4, -1}
    x := 3
    k := 2
    result := minOperations(nums, x, k)
    fmt.Println(result)
}