你是否曾好奇华为的自动驾驶汽车是如何感知周围环境、确定自身位置,并做出智能决策以抵达目标地点的?

它所使用的方法被称为SLAM。
SLAM,即“同步定位与建图”(Simultaneous Localization and Mapping),是机器人学和三维计算机视觉领域中的一个广为人知的术语。它是机器人感知系统的核心组成部分,使机器人能够在未知环境中自主导航。简而言之,SLAM 是一种让机器人在未知环境中同时确定自身位置并构建环境地图的方法。
在本文中,我将聚焦于感知模块,特别是其中的定位部分。我将逐步讲解单目视觉SLAM,并使用Python和OpenCV实现一个简易版本。我会将其中涉及的数学原理逐一拆解,以便更易于理解。最后,我还会简要介绍ORB-SLAM以及如何运行它。
如果你是机器人领域的初学者,我建议先阅读我之前发布的《机器人学的工程原理与应用》文章。该文介绍了机器人领域的最新进展、机器人自动化的核心组成部分、工业界与学术界常用的机器人工具,以及相关的职业机会。
机器人学的工程原理与应用
相信到此你已经清楚本文的目标了,那么现在就让我们动手实践吧!
什么是SLAM?
SLAM 的直观理解可以通过以下类比来说明:
想象你身处一个完全黑暗的房间,手中只有一支手电筒,每次只能照亮一小片区域。为了在房间中移动,你必须一边根据当前照亮的区域确定自己的位置(定位),一边在移动过程中记住所遇到物体的位置和特征,从而逐步构建出整个房间的地图(建图)。
通常,解决定位(Localization)问题有两种方式:
先建图后定位(Mapping then Localizing):
先构建环境的地图(mapping),之后利用这张地图来估计机器人的位置(位姿,pose)。在已有地图上进行定位比SLAM更高效。
SLAM(同步定位与建图):
在机器人移动过程中,同时创建地图并估计其在该地图中的位置。SLAM的计算开销比“先建图后定位”更大。
从构建鲁棒性解决方案的角度来看,SLAM显得更为有效,因为每次遇到未知环境都重新建图是低效的。
注意:
“位姿”(Pose)精确地指六自由度(6 Degrees of Freedom, 6DoF):[x, y, z, r, p, y]。其中 (x, y, z) 是笛卡尔坐标,(r, p, y) 是三维空间中的欧拉角(分别代表滚转、俯仰和偏航)。
本文中,“相机位姿”和“机器人位姿”可互换使用,均表示机器人在三维坐标系中的位置与朝向。
什么是视觉SLAM(Visual SLAM)?
当我们将相机作为SLAM算法的输入时,就称为视觉SLAM。
如果仅使用单个相机,则称为单目视觉SLAM(Monocular Visual SLAM)。
如果使用两个或多个相机(如立体相机阵列),则称为立体视觉SLAM(Stereo Visual SLAM)。
下面我们简要对比立体SLAM与单目视觉SLAM的主要优缺点。需要注意的是,本文将聚焦于单目SLAM,但后续系列文章中可能会介绍立体SLAM的实现。
|
方面 |
立体SLAM(Stereo SLAM) |
单目视觉SLAM(Monocular SLAM) |
|---|---|---|
| 轨迹估计 |
✅ 可以以米为单位精确估计轨迹 |
❌ 轨迹仅能估计到一个尺度因子(scale ambiguity) |
| 鲁棒性 |
✅ 通常更鲁棒(数据更多) |
❌ 数据点较少,可能不够鲁棒 |
| 计算复杂度 |
❌ 计算需求更高 |
✅ 计算需求较低 |
| 3D建图能力 |
❌ 需要两个相机及标定 |
✅ 仅需一个相机,设置更简单 |
| 3D重建细节 |
✅ 生成准确且稠密的3D地图 |
❌ 生成的地图精度较低、较稀疏 |
| 环境适应性 |
✅ 更擅长捕捉细节和深度信息 |
❌ 在细节和深度精度方面表现较差 |
| 系统设置复杂度 |
❌ 可能受双相机间光照差异影响 |
✅ 单相机设置性能更一致 |
表1:立体SLAM与单目SLAM对比
什么是单目SLAM(Monocular SLAM)?
问题形式化(Problem Formulation)
我们已经对单目视觉SLAM有了直观理解,现在来看它的数学表述。
输入:
给定从时间 (t = 0) 到 (t = n) 的一系列环境相机图像帧,表示为:
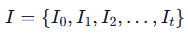
输出:
相机(即机器人)的轨迹:
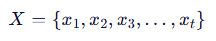
其中 (x_t) 表示时刻 (t) 的相机位姿。
环境的地图:
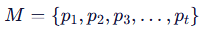
其中 (p_t) 表示环境中的三维点坐标。
目标:
在给定视觉观测 (I) 的条件下,最大化轨迹 (X) 和地图 (M) 的联合后验概率:
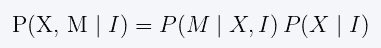
这里的后验概率是指在观测数据已知的情况下,事件发生的概率——这正是贝叶斯定理左侧的形式。
单目视觉SLAM可分解为两个子问题:
建图(Mapping)
:(P(M | X, I)) —— 在已知轨迹 (X) 和图像序列 (I) 的条件下,地图 (M) 的后验概率。
里程计(Odometry)
:(P(X | I)) —— 在已知视觉数据 (I) 的条件下,相机(机器人)轨迹 (X) 的后验概率。
单目视觉SLAM算法概览:它是如何工作的?
单目SLAM的工作流程可大致分为两类算法模块:前端(Front-end) 和 后端(Back-end)。
前端算法(Front-end Algorithms):
负责估计相机位姿和三维地图点(例如通过特征提取、匹配、三角化等)。
后端算法(Back-end Algorithms):
负责对前端估计出的位姿和地图进行优化(例如使用图优化、Bundle Adjustment 等方法),以提高整体精度和一致性。
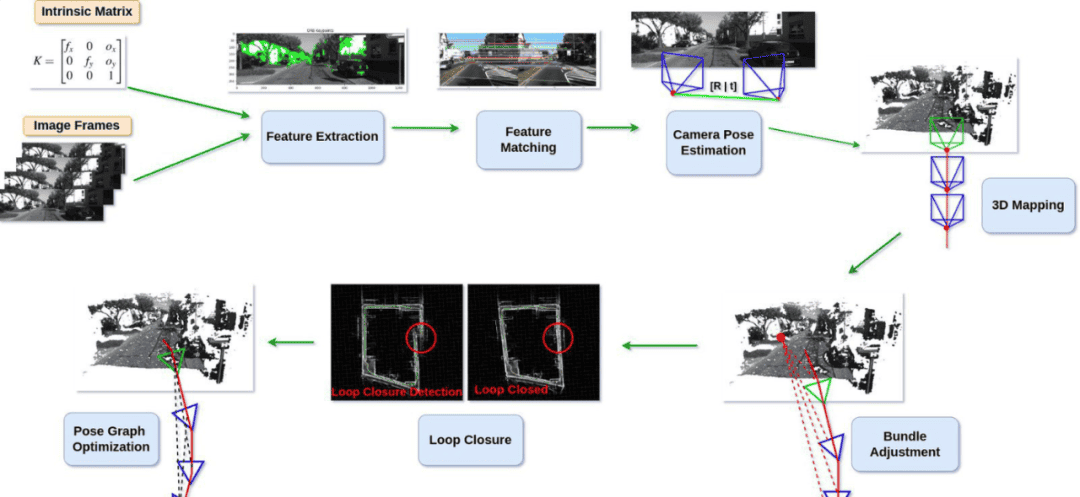
首先,相机会捕获两帧图像 (I_t) 和 (I_{t+1}),然后对这两幅图像进行去畸变(Undistort)处理。接着,应用以下前端算法来估计相机位姿和三维地图,再利用后端算法对先前估计的位姿和地图点进行优化。下面我详细说明这一过程:
前端算法(Front-end Algorithms):
特征提取(Feature Extraction):
在获取图像 (I_t) 和 (I_{t+1}) 后,分别对两幅图像进行特征提取。设从 (I_t) 和 (I_{t+1}) 中提取出的特征点集分别为 (F_t) 和 (F_{t+1})。
特征匹配(Feature Matching):
接下来,在 (F_t) 和 (F_{t+1}) 之间寻找特征点的对应关系。这种匹配也可以通过特征跟踪(feature tracking)的方式实现,即从图像 (I_t) 到 (I_{t+1}) 跟踪相同的特征点。
位姿估计(Pose Estimation):
利用匹配或跟踪得到的特征点,结合对极几何(epipolar geometry)计算相邻帧之间的相对相机位姿。对极几何需要输入两帧中的对应点以及相机的内参矩阵。
三角化(Triangulation):
利用估计出的相对相机位姿和对应的二维特征点,通过三角化方法重建周围环境的三维坐标。
局部建图(Local Mapping):
随着相机移动,不断累积估计出的三维点,逐渐形成一个局部地图(Local Map),反映相机所经过区域的环境结构。
完成初步的相机位姿和三维地图点估计后,我们进入后端优化阶段。
后端算法(Back-end Algorithms):
光束法平差(Bundle Adjustment):
通过最小化所有观测点的重投影误差(reprojection error),联合优化相机位姿和三维地图点,从而提高整体精度。
回环检测(Loop Closure Detection):
当相机再次回到之前访问过的位置时,系统需识别出这一“回环”。通常采用词袋模型(Bag-of-Words)或地点识别(place recognition)等技术来检测是否曾到过该位置。检测结果随后用于位姿图优化。
位姿图优化(Pose Graph Optimization):
一旦检测到回环,系统会执行位姿图优化,对整个轨迹和地图进行全局调整,以消除累积误差,确保地图的全局一致性(global consistency)。
如果你对上面提到的所有步骤还不太理解,不必担心。接下来的正文会用通俗易懂的语言,对每个要点进行详细而清晰的解释。
前端算法
特征提取(Feature Extraction)
特征是对图像信息的一种数字化表达。一组高质量的特征对于最终任务的性能至关重要,因此多年来研究人员在特征提取方面开展了大量深入的工作。
在经典计算机视觉中,这类特征与深度学习中的特征有所不同。经典方法中的特征是人工设计(handcrafted)的,通常以特征点(feature points)的形式表示——即图像中某些具有代表性的特殊位置。以下图为例,我们可以将图像中的角点、边缘和色块等视为典型的代表性区域。
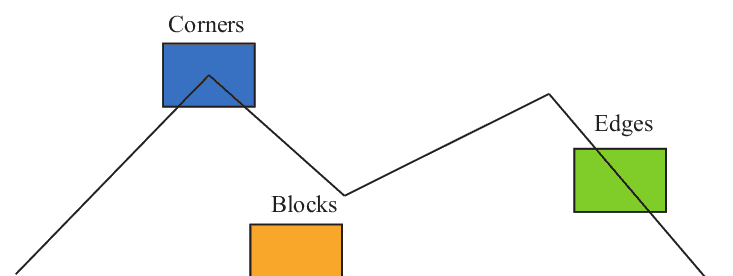
一个特征点由两部分组成:关键点(key point)和描述子(descriptor)。
关键点(key point):
关键点指的是特征点在图像中的二维位置。某些类型的关键点还包含其他信息,例如方向(orientation)和尺度(size)。
描述子(descriptor):
描述子通常是一个向量,用于描述关键点周围像素的信息。描述子的设计应满足:外观相似的特征具有相似的描述子。因此,如果两个特征描述子在向量空间中距离很近,就可以认为它们代表的是同一个特征。

SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)是最著名的经典特征提取算法之一,以其高精度和强鲁棒性著称。然而,SIFT 的计算量较大,导致其计算开销较高。相比之下,ORB(Oriented FAST and Rotated BRIEF)特征则广泛应用于实时特征提取场景。ORB 结合了改进版的 FAST 角点检测器(称为 Oriented FAST)与极快的二进制描述子 BRIEF,大幅加速了整个图像特征提取过程。
代码:
以下是使用 ORB 进行特征提取的 OpenCV Python 代码:
# 初始化 ORB 检测器,设置最多提取 5000 个关键点orb = cv2.ORB_create(nfeatures=5000)# 检测关键点并计算描述子keypoints, descriptors = orb.detectAndCompute(image, None)

ORB 特征提取原理解析:
ORB 特征提取的核心思想是:如果一个像素与其邻近像素的亮度差异很大(明显更亮或更暗),那么它很可能是角点。其完整流程如下:
在图像中选取一个像素 (p),假设其亮度为 (I_p)。
设定一个阈值 (T)(例如,取 (I_p) 的 20%)。
以像素 (p) 为中心,在半径为 3 的圆周上选取 16 个像素点。
如果这 16 个圆周像素中有连续 (N) 个点的亮度大于 (I_p + T) 或小于 (I_p – T),则认为中心像素 (p) 是一个特征点。通常,(N) 的取值为 12、11 或 9。
对图像中的每个像素重复上述四个步骤,即可完成特征点检测。

为了提高效率,ORB 采用了一个小技巧:先检查圆周上位置 1、9、5 和 13 的四个像素点。只有当这四个点中至少有 (N) 个的亮度大于 (I_p + T) 或小于 (I_p – T) 时,才将该中心像素视为候选角点。这一策略能快速排除大量非角点,显著提升检测速度。
你可能现在还不清楚这与单目SLAM有什么关系,但请耐心继续阅读。随着后续内容的展开,你会逐渐把这些知识点串联起来。
特征点提取匹配相关的教学视频
特征匹配(Feature Matching)
特征匹配紧接在特征提取之后,是视觉SLAM中的关键步骤,用于在连续两帧图像之间寻找匹配的特征点。
用计算机视觉的术语来说,就是在这两幅图像中建立特征对应关系。例如,假设第 (I) 帧中有特征集 (F_1),第 (I+1) 帧中有特征集 (F_2),我们需要找出它们之间的匹配对。
具体做法如下:
对第 (I) 帧中的每个特征点,计算它与第 (I+1) 帧中所有特征点的平方差和(Sum of Squared Differences, SSD)。
找出距离最小(最佳匹配)和次小(次佳匹配)的两个匹配点,并计算它们的距离比值(即最佳匹配距离除以次佳匹配距离)。
如果该比值低于某个预设阈值,则保留这对匹配;否则予以剔除。
这一过程(通常称为“最近邻距离比测试”,NNDR)能够有效筛选出高置信度的特征对应关系,这些可靠的匹配点随后被用于估计相机在世界坐标系中的旋转和平移(即相对位姿)。

这段代码首先初始化一个 ORB 检测器,用于在两幅图像中检测关键点并计算描述子;然后使用
cv2.BFMatcher()
代码:
# 初始化 ORB 检测器orb = cv2.ORB_create(nfeatures=1000)# 在第一幅图像中检测关键点并计算描述子keypoints1, descriptors1 = orb.detectAndCompute(image1, None)# 在第二幅图像中检测关键点并计算描述子keypoints2, descriptors2 = orb.detectAndCompute(image2, None)# 使用默认参数初始化暴力匹配器(BFMatcher)bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)# 匹配第 I 帧与第 I+1 帧之间的描述子matches = bf.match(descriptors1, descriptors2)# 按匹配距离排序(距离越小表示匹配越好)matches = sorted(matches, key=lambda x: x.distance)

特征跟踪(Feature Tracking)可以用来替代特征匹配,用于在连续帧之间追踪关键点。相比匹配,跟踪关键点的计算效率更高,这对于实时应用至关重要。然而,在某些情况下跟踪可能会失败,例如:运动幅度过大、误差累积导致的漂移,以及特征对应关系丢失等。
以下是从第 (I) 帧到第 (I+1) 帧跟踪特征点的代码。在
cv2.calcOpticalFlowPyrLK
代码:
# Lucas-Kanade 光流法的参数设置lk_params = dict(winSize=(15, 15),maxLevel=2,criteria=(cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 0.03))# 计算稀疏光流(从 image1 到 image2)points2, status, err = cv2.calcOpticalFlowPyrLK(image1, image2, points1, None, **lk_params)# 筛选出成功跟踪的点good_new = points2[status.ravel() == 1] # 第 I+1 帧中的有效点good_old = points1[status.ravel() == 1] # 第 I 帧中对应的原始点

位姿估计(Pose Estimation)
相机位姿估计非常重要,因为只有在完成位姿估计之后,才能进一步重建三维地图。位姿估计涉及大量数学计算。要理解这一主题,我们首先需要掌握一些基础知识,并熟悉常用术语。
首先,让我们了解世界坐标系、相机坐标系和图像坐标系,以及如何将三维空间中的物体投影到二维图像上(即成像过程),还有对极几何(Epipolar Geometry)等相关概念。
世界坐标系(World Coordinate Frame, WCF)
世界坐标系是计算机视觉、机器人学和三维图形学中使用的一种全局参考坐标系,用于定义场景中物体的位置和朝向。你可以将环境中任意一个三维位置设为世界坐标系的原点。例如,一台需要在大学校园内运行的机器人,可以将校门作为其世界坐标系的原点。
相机坐标系(Camera Coordinate Frame)
假设你在世界坐标系中的某个位置放置了一台相机。如果以该相机的位置作为原点,并以此为参考来描述环境中任意物体的位置,那么这个坐标系就称为相机坐标系。
世界坐标系与相机坐标系之间的关系(3D 到 3D 的变换)由一组参数定义,这些参数构成外参矩阵(Extrinsic Matrix)([R | t]),其中 (R) 是旋转矩阵,(t) 是平移向量。该矩阵用于在世界坐标系和相机坐标系之间进行坐标转换——既可将世界坐标转换到相机坐标,也可反向转换。
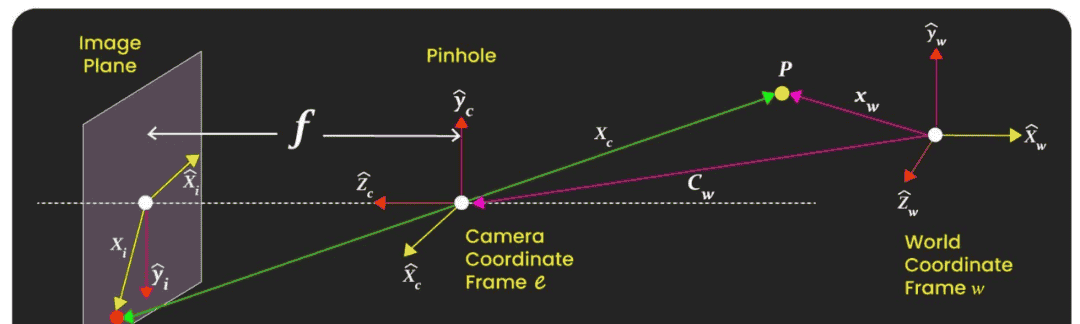
图像坐标系(Image Coordinate Frame)
图像坐标系是图像本身的二维坐标系。从三维空间到二维图像的转换通过透视投影(Perspective Projection)实现。图像坐标系与相机坐标系之间的关系由相机的内参(intrinsic parameters)决定,这些参数通常组成一个称为内参矩阵(Intrinsic Matrix,记作 (K))的矩阵。
如果你觉得这些矩阵和坐标系的概念目前还难以理解,只需记住一点:相机有两个关键矩阵——外参矩阵和内参矩阵。
首先,利用外参矩阵将世界坐标系中的三维点转换到相机坐标系中(3D → 3D);
然后,再通过内参矩阵将相机坐标系中的点投影到图像平面(即图像坐标系)上(3D → 2D)。
后续内容将帮助你更深入、更清晰地理解这一过程。
成像原理详解(Image Formation Explained)
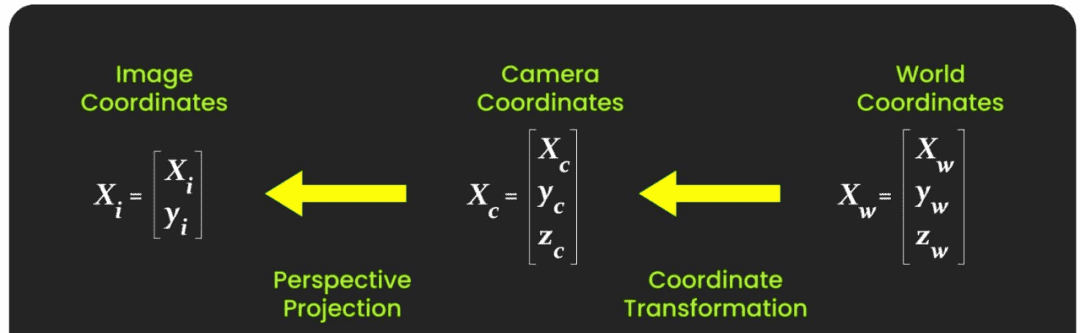
当我们拍摄一张图像时,物体的三维点首先被转换到相机坐标系中。这是一个3D 到 3D 的变换,通过外参矩阵(Extrinsic Matrix)实现。其数学表达式如下:

注意:(R) 和 (t) 描述的是相机坐标系相对于世界坐标系的旋转和平移。
一旦物体点被表示在相机坐标系中,我们便使用内参矩阵 (K),将该三维点投影到二维图像平面上,完成从 3D 到 2D 的变换:

对极几何详解(Epipolar Geometry Explained)
在单目相机(monocular camera)的情况下,我们只能获得特征点的二维像素坐标。因此,核心问题是如何仅根据两组二维点来估计相机的运动和场景的深度。这个问题正是通过对极几何(Epipolar Geometry)来解决的。
你可能会疑惑:对极几何通常是在双目视觉(stereo vision)文章中讲授的,为什么在单目SLAM(Monocular SLAM)的上下文中也要讨论它?
原因在于:仅凭单张图像无法恢复深度信息。要估计深度,必须利用多帧图像。在单目SLAM中,我们通过不同时间戳拍摄的连续图像帧来重建三维结构,而对极几何正是连接这些帧、推断深度和相对位姿的关键工具——因此它在单目SLAM中至关重要。
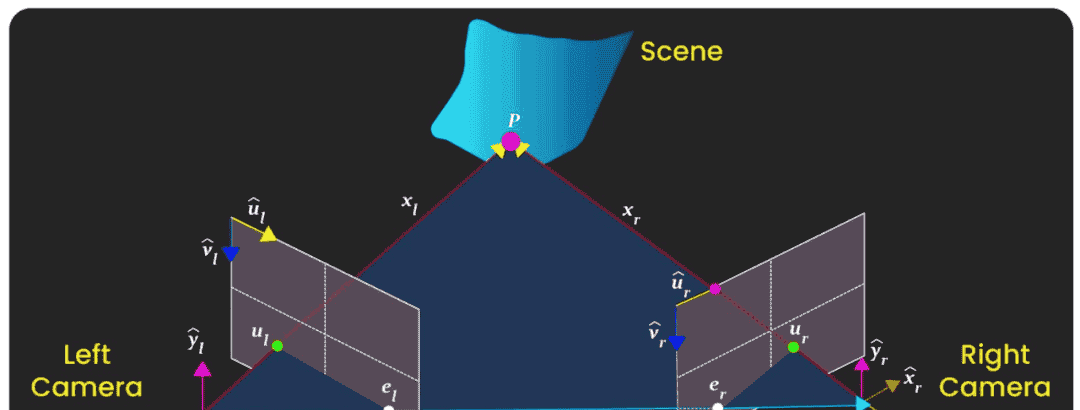
对极几何(Epipolar Geometry)描述了同一三维场景在两个不同相机视角下的图像之间的几何关系。
由两个相机的光心 (O_l) 和 (O_r) 以及空间中某一点 (P) 所确定的平面称为对极平面(epipolar plane)。该平面与左右两个图像平面的交线即为对极线(epipolar lines)(l_1) 和 (l_2)。这些对极线限定了对应点可能出现的位置,从而将匹配搜索从二维空间简化为一维(只需沿对极线搜索)。
对极点(epipoles)(e_l) 和 (e_r) 是连接两个相机光心的基线(baseline)与各自图像平面的交点。
为了确定从左帧 (I_l) 到右帧 (I_r) 之间的运动(由旋转 (R) 和平移 (t) 描述),必须确保左图中的特征点 (u_l) 与右图中的点 (p_r) 正确对应——即它们是由同一个三维点 (P) 投影而来。这一几何约束被封装在基础矩阵(Fundamental Matrix)(F) 中,该矩阵在特征匹配和三维重建任务中起着关键作用。
在继续深入之前,我们先了解对极几何中的几个重要公式。

其中:
(X_l):三维点在左相机坐标系中的坐标
(X_r):三维点在右相机坐标系中的坐标
(R):从右相机到左相机的旋转矩阵
(t):从右相机到左相机的平移向量
(E):本质矩阵(Essential Matrix)
(u_l):左图像中像素坐标的 x 分量
(v_l):左图像中像素坐标的 y 分量
(f_x, f_y):相机在 x 和 y 方向的焦距(以像素为单位)
(x_l, x_r):左右图像中对应点的齐次坐标(2D 像素坐标)
(z_l):该点在左相机坐标系中的深度(z 坐标)
(O_x, O_y):图像主点(光学中心)的像素坐标
(K_l, K_r):左右相机的内参矩阵
(F):基础矩阵(Fundamental Matrix)
给定一组少量的对应点(例如仅需 8 对点,这些点来自前面步骤 1 和 2 中提取并匹配的特征点),我们可以通过求解方程 (
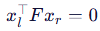
) 来估计基础矩阵 (F)。该问题可写成如下矩阵形式:
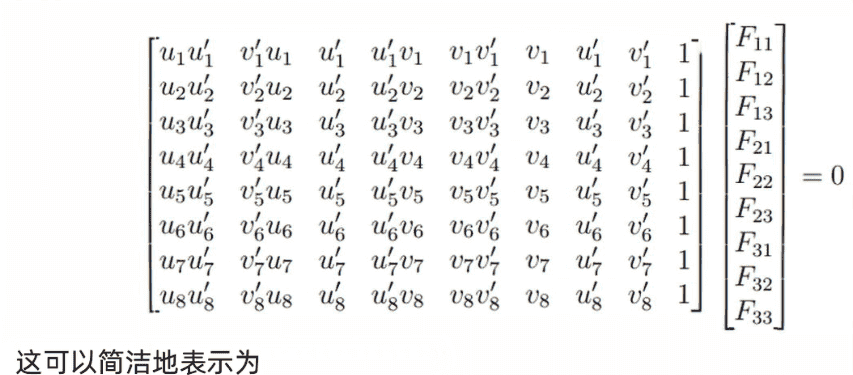
这里,(W) 是一个从 (N)((N) ≥ 8)个对应点中导出的 (N imes 9) 矩阵,而 (f) 是我们希望求得的基础矩阵 (F) 的值。
上述方程组可以通过奇异值分解(SVD)来解决线性最小二乘问题。找到 (F) 的值之后,我们可以将其用于第6个方程来计算本质矩阵 (E) 的值。随后,可以对 (E) 进行SVD分解以估计旋转 (R) 和平移 (t)。
以下代码示例展示了如何从两个图像中提取匹配的关键点,设置相机的内参参数,并使用RANSAC(随机抽样一致性)方法计算基础矩阵 (F),以稳健地估计哪些匹配是内点(inliers)。
代码:
# 提取匹配的关键点pts1 = np.float32([keypoints1[m.queryIdx].pt for m in matches])pts2 = np.float32([keypoints2[m.trainIdx].pt for m in matches])# 相机内参参数(示例值,请替换为你的相机校准数据)K = np.array([[fx, 0, cx],[0, fy, cy],[0, 0, 1]])# 使用RANSAC计算基础矩阵F, inliers = cv2.findFundamentalMat(pts1, pts2, cv2.FM_RANSAC)# 使用相机的内参参数计算本质矩阵E = K.T @ F @ K# 分解本质矩阵以获取 R 和 t_, R, t, mask = cv2.recoverPose(E, pts1[inliers.ravel()==1], pts2[inliers.ravel()==1], K)
在实际应用中,由于不正确的对应、噪声或遮挡等原因,特征匹配通常包含异常值(错误的对应)。RANSAC 方法有助于识别并排除这些异常值,从而更准确地计算本质矩阵。在估算出本质矩阵的值后,如第3个方程所述,我们可以使用 SVD 分解它以得到 (R) 和 (t)。三角化(Triangulation)
在前一步骤中,我们介绍了使用对极约束来估计相机运动,并讨论了它的局限性。在估计了运动之后,下一步是利用相机运动来估计特征点的空间位置。在单目SLAM中,仅凭一张图像无法获得像素的深度信息。我们需要通过三角化的方法来估计地图点的深度。
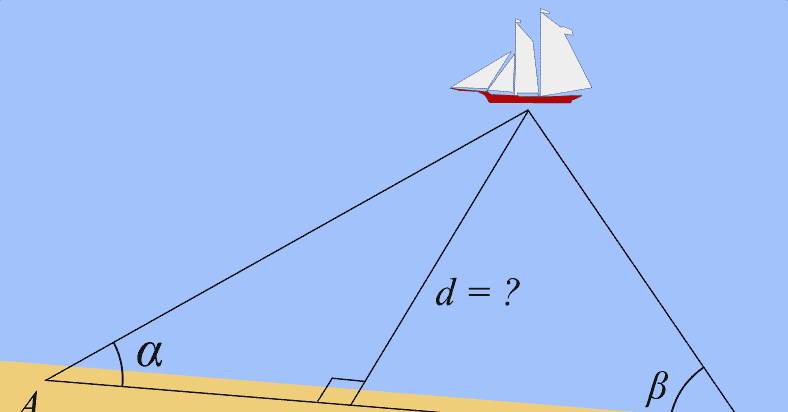
三角化(Triangulation)是一种历史悠久的经典方法,过去常用于确定某一点的地理定位。
在对极几何中使用的三角化方法与地理定位中的三角化基于相似的核心思想,例如:
两种方法都利用三角测量原理,通过已知的参考点和观测数据来确定未知位置;
两者都涉及几何计算,以求解空间中多条视线(或射线)的交点。
不过,对极几何中的三角化有所不同:它依赖于图像间的对应点以及相机的标定参数(内参和外参)。
为了估算一个物体点的三维坐标,三角化过程如下:

此处,矩阵 (A) 是由 (mathbf{x}_1)、(P_1)、(mathbf{x}_2) 和 (P_2) 的分量构建而成。该齐次线性方程组的解通常通过线性最小二乘法求得,常用方法是奇异值分解(SVD),以获得三维点 (mathbf{X}) 的最优估计。
代码:
import numpy as npdef add_ones(pts):"""辅助函数:为二维数组添加一列1,转换为齐次坐标。"""return np.hstack([pts, np.ones((pts.shape[0], 1))])def triangulate(pose1, pose2, pts1, pts2):# 初始化结果数组,用于存储3D点的齐次坐标ret = np.zeros((pts1.shape[0], 4))# 对相机位姿求逆,得到从相机坐标系到世界坐标系的变换(即投影矩阵的逆)pose1 = np.linalg.inv(pose1)pose2 = np.linalg.inv(pose2)# 遍历每一对匹配点for i, p in enumerate(zip(add_ones(pts1), add_ones(pts2))):# 初始化矩阵 A,用于存放由投影关系导出的线性方程A = np.zeros((4, 4))# 根据投影矩阵和图像点构造方程A[0] = p[0][0] * pose1[2] - pose1[0]A[1] = p[0][1] * pose1[2] - pose1[1]A[2] = p[1][0] * pose2[2] - pose2[0]A[3] = p[1][1] * pose2[2] - pose2[1]# 对 A 进行 SVD 分解_, _, vt = np.linalg.svd(A)# 解为 V^T 的最后一行(对应最小奇异值的右奇异向量)ret[i] = vt[3]# 返回齐次坐标形式的3D点return ret
第12行和第13行中的矩阵求逆操作是必要的,因为输入的 pose1 和 pose2 通常是从世界坐标系到相机坐标系的 机坐标系的变换(即外参矩阵 ([R|t]))。为了进行三角化,我们需要其逆变换——即将相机坐标系中的射线反投影回世界坐标系。

局部建图(Local Mapping)
在视觉SLAM中,局部建图是指利用最近观测所生成的新三维点来更新局部地图。这些通过三角化得到的新点会被加入到局部地图中。系统会从中选择一些关键帧(Keyframes)来代表具有重要意义的相机位置。
在视觉SLAM中,关键帧不仅指在某一时刻捕获的图像,还包括该时刻对应的相机位姿(即位置和朝向)。关键帧与普通帧的主要区别在于:关键帧通常包含大量检测到的特征点(关键点),这些特征点被用于地图构建和位姿估计。并非所有捕获的普通帧都会被保留,只有其中一部分满足特定条件的帧才会被选为关键帧。
后端算法(Back-end Algorithms)
光束法平差(Bundle Adjustment)
光束法平差是一个概念上非常简单、但在SLAM和运动恢复结构(Structure from Motion, SfM)领域被广泛使用的技术。
光束法平差是一种用于三维重建的优化过程,旨在同时优化场景中三维点的位置以及拍摄这些点的相机的位置和朝向(姿态)。
该过程通过最小化重投影误差(reprojection error)来实现——即图像中实际观测到的特征点位置与根据当前三维模型和相机参数所预测的位置之间的差异。减小这一误差有助于构建更精确的三维地图,并获得更准确的相机轨迹。
光束法平差与梯度下降法类似,二者都属于优化技术,目标都是最小化某种误差度量。在梯度下降中,算法通过迭代调整参数(例如神经网络中的权重)来缩小预测值与真实值之间的差距;而在光束法平差中,算法则通过迭代优化三维点坐标和相机位姿,以最小化重投影误差。
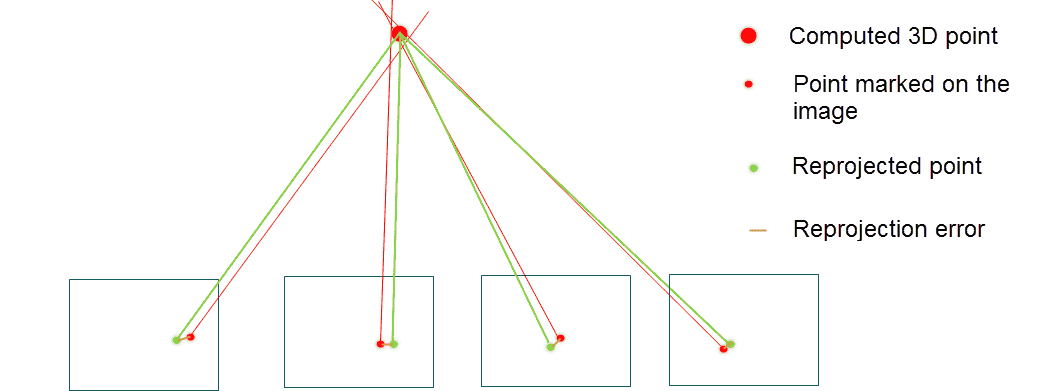
代码:
def vertex_to_points(optimizer, first_point_id, last_point_id):""" Converts g2o point vertices to their current 3d point estimates. """vertices_dict = optimizer.vertices()estimated_points = list()for idx in range(first_point_id, last_point_id):estimated_points.append(vertices_dict[idx].estimate())estimated_points = np.array(estimated_points)xs, ys, zs = estimated_points.Treturn xs, ys, zsipv.show()for i in range(100):optimizer.optimize(1)xs, ys, zs = vertex_to_points(optimizer, first_point_id, last_point_id)scatter_plot.x = xsscatter_plot.y = ysscatter_plot.z = zstime.sleep(0.25)

代码:
# 计算重投影误差的函数def compute_reprojection_error(intrinsics, extrinsics, points_3d, observations):total_error = 0 # 初始化总误差为零num_points = 0 # 初始化点的数量为零# 遍历每个相机的外参矩阵和对应的2D观测点for (rotation, translation), obs in zip(extrinsics, observations):# 使用当前相机的内参和外参将3D点投影到2D平面projected_points = project_points(points_3d, intrinsics, rotation, translation)# 计算投影点与观测点之间的欧几里得距离(重投影误差)error = np.linalg.norm(projected_points - obs, axis=1)# 累加总误差total_error += np.sum(error)# 累加总点数num_points += len(points_3d)# 计算平均重投影误差mean_error = total_error / num_pointsreturn mean_error # 返回平均重投影误差
回环检测(Loop Closure Detection)
回环是后端使用的一种算法。回环检测使系统能够识别机器人何时返回到之前访问过的位置,从而在其路径上有效地闭合循环。这种能力对于精确的地图构建和定位至关重要,因为它有助于减少随着时间积累的漂移误差。
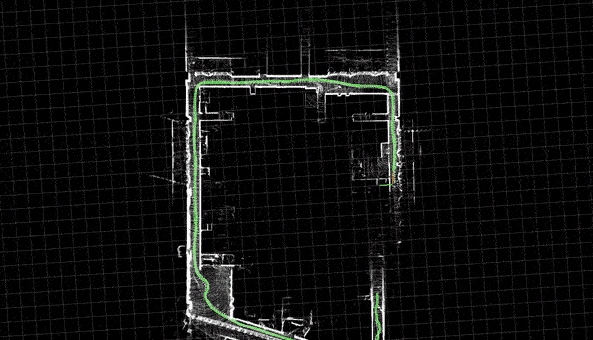
SLAM 系统维护一个图结构,其中节点表示相机位姿,边表示空间约束关系。当检测到闭环时,系统会向图中添加新的边,以表示新识别出的位置关联,并应用诸如位姿图优化(Pose Graph Optimization)或光束法平差(Bundle Adjustment)等优化技术,以最小化整体误差。
词袋模型(Bag-of-Words, BoW)是一种用于视觉 SLAM 中闭环检测的地点识别算法。它将图像特征转换为一组“视觉单词”的向量,从而生成紧凑的图像描述子。在闭环检测过程中,当前图像的 BoW 描述子会与之前访问过的位置所存储的描述子进行比对。若两个描述子之间具有较高的相似性,则表明当前位置已被访问过,系统便可高效且准确地检测到闭环,即使在大规模环境中也能有效工作。
DBoW2 是一个开源的 C++ 库,用于将图像索引并转换为词袋表示。该库也被 ORB-SLAM 等主流 SLAM 系统所采用。
位姿图优化(Pose Graph Optimization)
位姿图优化是视觉 SLAM 后端的关键步骤,用于优化相机(或机器人),从而保证地图的全局一致性。这一优化至关重要,因为在建图过程中,微小的位姿估计误差会随时间不断累积,最终导致显著的轨迹漂移。位姿图优化通过同时优化整条轨迹上的所有位姿来校正这些误差。
当检测到闭环时,位姿图优化会将闭环所提供的约束信息融入图中,调整相关位姿,从而有效减少漂移。
位姿图优化 与 光束法平差 的区别
位姿图优化听起来可能与光束法平差类似,但二者目标不同:
光束法平差
同时优化三维点坐标和相机位姿,目标是最小化重投影误差;
位姿图优化
则仅优化相机位姿,不涉及三维点的调整。
基于 Python 和 OpenCV 的简易单目视觉 SLAM
目前互联网上可用的 Python 实现较少,主要是因为其效率较低,难以满足实时性要求。然而,从教学和学习的角度来看,Python 实现具有重要价值——它们为初学者提供了理解 SLAM 原理的良好起点。

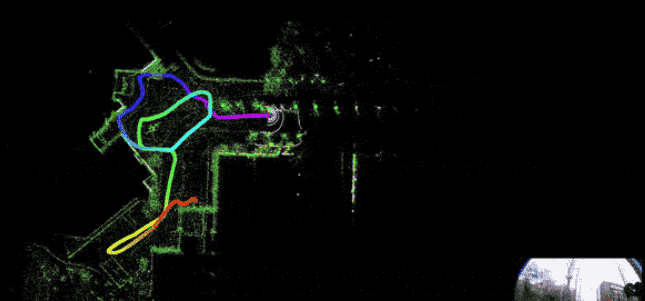
出于这一原因,我们将一起学习一个仅包含4个文件的简易单目视觉SLAM Python实现。该实现主要涵盖视觉SLAM的前端部分,即相机位姿估计和三维地图构建。上图1(d)即为该Python实现的输出结果。
看起来很酷!接下来我们来理解它是如何实现的。
代码结构如下,仅包含4个Python文件和一个测试视频。虽然这不是最精确的单目视觉SLAM实现,但其结果已相当不错。让我们先看一下文件结构:
├── display.py├── extractor.py├── main.py├── pointmap.py└── test_countryroad.mp4
extractor.py:包含用于估计相机位姿的各种工具函数,例如:
特征提取(
extract
特征匹配(
match_frames
相机位姿估计(
extractPose
坐标归一化与反归一化(
normalize
denormalize
定义关键帧的类(
Frame
display.py:使用名为 Simple DirectMedia Layer (SDL2) 的库实现图像可视化。
pointmap.py:使用 Pangolin 库实现三维点云和地图的可视化。
main.py:读取视频文件及其相机内参矩阵,并调用其他文件中的函数进行三维建图和相机位姿估计。
注意:我们在每段代码之后都会解释其中的类和函数,但同时也请务必阅读代码中的注释——那里通常有更清晰的说明。
main.py 的详解
我们逐个文件来看,首先从 main.py 开始:
import cv2from display import Displayfrom extractor import Frame, denormalize, match_frames, IRt, add_onesimport numpy as npfrom pointmap import Map, Point### 相机内参# 定义主点(光心)坐标W, H = 1920//2, 1080//2# 定义焦距F = 270# 定义内参矩阵及其逆矩阵K = np.array([[F, 0, W//2],[0, F, H//2],[0, 0, 1]])Kinv = np.linalg.inv(K)# 初始化图像显示窗口display = Display(W, H)# 初始化地图mapp = Map()mapp.create_viewer()
在导入依赖之后,我们定义了一些在整个代码中频繁使用的重要参数,包括:光心坐标(principal point)
焦距(focal length)
相机内参矩阵 ( K ) 及其逆矩阵 ( K^{-1} )
三维地图对象
图像显示窗口
接下来是核心函数
process_frame
def process_frame(img):img = cv2.resize(img, (W, H))frame = Frame(mapp, img, K)if frame.id == 0:return# 当前帧 f1 与前一帧 f2f1 = mapp.frames[-1]f2 = mapp.frames[-2]idx1, idx2, Rt = match_frames(f1, f2)# X_f1 = R * X_f2 + t,将 f2 的位姿转换到 f1 的坐标系下f1.pose = np.dot(Rt, f2.pose)# 对极几何三角化:输出为齐次坐标下的3D点,形状为 (n, 4)pts4d = triangulate(f1.pose, f2.pose, f1.pts[idx1], f2.pts[idx2])# 转换为欧氏坐标(除以齐次坐标最后一维 W)pts4d /= pts4d[:, 3:]# 剔除视差不足或位于相机后方的点good_pts4d = (np.abs(pts4d[:, 3]) > 0.005) & (pts4d[:, 2] > 0)for i, p in enumerate(pts4d):if not good_pts4d[i]:continuept = Point(mapp, p)pt.add_observation(f1, i)pt.add_observation(f2, i)# 在图像上绘制特征点和匹配轨迹for pt1, pt2 in zip(f1.pts[idx1], f2.pts[idx2]):u1, v1 = denormalize(K, pt1)u2, v2 = denormalize(K, pt2)cv2.circle(img, (u1, v1), 3, (0, 255, 0))cv2.line(img, (u1, v1), (u2, v2), (255, 0, 0))# 2D 显示display.paint(img)# 3D 显示mapp.display()if __name__ == "__main__":cap = cv2.VideoCapture("/path/to/car.mp4")while cap.isOpened():ret, frame = cap.read()if ret:process_frame(frame)else:break
注:
triangulate
process_frame
if frame.id == 0: return
非常关键,因为仅凭第一帧无法进行任何位姿或地图估计。
获取当前帧
f1
f2
match_frames
进行特征匹配,找出两帧之间的对应点。
利用
Rt
f2
f1
f1
使用三角化计算三维地图点。
将齐次坐标转换为欧氏坐标(除以 ( W ))。
剔除视差过小(< 0.005)或位于相机后方(Z ≤ 0)的无效点。
若点有效,则将其加入地图,并记录其在两帧中的观测。
对所有有效匹配点进行反归一化,绘制特征点(绿色圆圈)和跟踪轨迹(蓝色连线)。
最后,同时显示2D图像和3D地图(含相机位姿)。
在
if __name__ == "__main__":
process_frame
extractor.py 的详解
你是否好奇
match_frames
denormalize
import cv2import numpy as npfrom skimage.measure import ransacfrom skimage.transform import FundamentalMatrixTransformimport g2odef add_ones(x):# 将点 x 转换为齐次坐标return np.concatenate([x, np.ones((x.shape[0], 1))], axis=1)
add_ones
:将二维或三维点转换为齐次坐标形式。
def extractPose(F):W = np.mat([[0, -1, 0], [1, 0, 0], [0, 0, 1]])U, d, Vt = np.linalg.svd(F)assert np.linalg.det(U) > 0if np.linalg.det(Vt) < 0:Vt *= -1R = np.dot(np.dot(U, W), Vt)if np.sum(R.diagonal()) < 0:R = np.dot(np.dot(U, W.T), Vt)t = U[:, 2]ret = np.eye(4)ret[:3, :3] = Rret[:3, 3] = tprint(d)return ret
extractPose
:通过奇异值分解(SVD)从基础矩阵 ( F ) 中恢复相对相机位姿(4×4 齐次变换矩阵),包含旋转 ( R ) 和平移 ( t )。
def extract(img):orb = cv2.ORB_create()pts = cv2.goodFeaturesToTrack(np.mean(img, axis=-1).astype(np.uint8),1000, qualityLevel=0.01, minDistance=10)kps = [cv2.KeyPoint(f[0][0], f[0][1], 20) for f in pts]kps, des = orb.compute(img, kps)return np.array([(kp.pt[0], kp.pt[1]) for kp in kps]), des
extract
:使用
goodFeaturesToTrack
def normalize(Kinv, pts):return np.dot(Kinv, add_ones(pts).T).T[:, 0:2]
normalize
:利用内参逆矩阵 ( K^{-1} ) 将像素坐标转换为归一化相机坐标(消除焦距和主点影响)。
def denormalize(K, pt):ret = np.dot(K, [pt[0], pt[1], 1.0])ret /= ret[2]return int(round(ret[0])), int(round(ret[1]))
denormalize
:将归一化坐标转换回像素坐标。
def match_frames(f1, f2):bf = cv2.BFMatcher(cv2.NORM_HAMMING)matches = bf.knnMatch(f1.des, f2.des, k=2)ret = []idx1, idx2 = [], []for m, n in matches:if m.distance < 0.75 * n.distance: # Lowe's ratio testp1 = f1.pts[m.queryIdx]p2 = f2.pts[m.trainIdx]if np.linalg.norm(p1 - p2) < 0.1: # 额外距离约束idx1.append(m.queryIdx)idx2.append(m.trainIdx)ret.append((p1, p2))assert len(ret) >= 8ret = np.array(ret)idx1 = np.array(idx1)idx2 = np.array(idx2)# 使用 RANSAC 拟合基础矩阵model, inliers = ransac((ret[:, 0], ret[:, 1]),FundamentalMatrixTransform,min_samples=8,residual_threshold=0.005,max_trials=200)ret = ret[inliers]Rt = extractPose(model.params)return idx1[inliers], idx2[inliers], Rt
match_frames
:
使用 BFMatcher 进行 ORB 描述子的 k 近邻匹配;
应用 Lowe’s ratio test(阈值 0.75)和额外的欧氏距离约束(< 0.1)筛选初步匹配;
使用 RANSAC 拟合基础矩阵,剔除外点;
从内点中恢复相对位姿 ( Rt );
返回内点索引和变换矩阵。
class Frame(object):def __init__(self, mapp, img, K):self.K = Kself.Kinv = np.linalg.inv(self.K)self.pose = IRt # 初始位姿(假设 IRt 已预定义为单位矩阵)self.id = len(mapp.frames)mapp.frames.append(self)pts, self.des = extract(img)self.pts = normalize(self.Kinv, pts)
Frame
类:初始化一帧,包含内参、位姿、归一化后的特征点及描述子,并自动加入全局地图。
通过这四个简洁的文件,我们构建了一个可运行的单目视觉SLAM原型,非常适合初学者理解SLAM前端的核心流程:特征提取 → 匹配 → 位姿估计 → 三角化建图 → 可视化。
pointmap.py 文件说明
让我们来理解一下在
pointmap.py
from multiprocessing import Process, Queueimport numpy as npimport pangolinimport OpenGL.GL as gl# 全局地图 // 使用 Pangolin 实现 3D 地图可视化class Map(object):def __init__(self):self.frames = [] # 相机帧(即相机位姿)self.points = [] # 地图中的 3D 点self.state = None # 用于保存当前地图和相机位姿状态的变量self.q = None # 用于进程间通信的队列;q 用于可视化进程def create_viewer(self):# 并行执行:创建此进程的主要目的是让 `viewer_thread` 方法与主程序并行运行。# 这样可以让 3D 查看器持续更新和渲染画面,而不会阻塞主程序的执行流程。self.q = Queue() # 初始化一个队列 q# 创建一个并行进程,目标函数为 `viewer_thread`# args 指定了该函数所需的参数p = Process(target=self.viewer_thread, args=(self.q,))# 设置为守护进程:当主程序退出时,该进程也会自动退出p.daemon = True# 启动进程p.start()def viewer_thread(self, q):# `viewer_thread` 接收队列 q 作为输入# 初始化可视化窗口self.viewer_init(1280, 720)# 无限循环,持续刷新查看器while True:self.viewer_refresh(q)def viewer_init(self, w, h):pangolin.CreateWindowAndBind('Main', w, h)# 启用深度测试,确保只渲染最近的物体,# 从而正确呈现场景中的遮挡关系,使画面更真实。gl.glEnable(gl.GL_DEPTH_TEST)# 设置相机的投影矩阵和模型视图矩阵self.scam = pangolin.OpenGlRenderState(# `ProjectionMatrix` 参数依次为:# 视口宽高 (w, h)、x 和 y 方向的焦距 (420, 420)、# 主点坐标 (w//2, h//2),以及近远裁剪平面 (0.2, 10000)。# 焦距决定了视场角,主点表示投影中心,# 裁剪平面定义了相机能渲染的距离范围——# 距离小于 0.2 或大于 10000 的物体会被裁剪掉。pangolin.ProjectionMatrix(w, h, 420, 420, w//2, h//2, 0.2, 10000),# `ModelViewLookAt` 设置相机视角矩阵,定义相机在 3D 场景中的位置和朝向。# 前三个参数 (0, -10, -8) 是相机的世界坐标位置;# 接下来三个参数 (0, 0, 0) 是相机注视的目标点(此处为原点);# 最后三个参数 (0, -1, 0) 是“上”方向向量,表示相机认为的“上方”方向(此处指向负 Y 轴)。# 这种设置将相机置于原点下方 10 单位、后方 8 单位处,# 注视原点,且“上”方向朝下,这种非常规设定可能是为了获得特定视角。pangolin.ModelViewLookAt(0, -10, -8, 0, 0, 0, 0, -1, 0))# 创建 3D 交互处理器self.handler = pangolin.Handler3D(self.scam)# 创建显示上下文self.dcam = pangolin.CreateDisplay()# 设置显示区域边界self.dcam.SetBounds(0.0, 1.0, 0.0, 1.0, -w/h)# 绑定交互处理器(支持鼠标操作等)self.dcam.SetHandler(self.handler)self.darr = Nonedef viewer_refresh(self, q):# 如果当前状态为空,或队列中有新数据if self.state is None or not q.empty():# 从队列中获取最新状态self.state = q.get()# 清除颜色缓冲区和深度缓冲区gl.glClear(gl.GL_COLOR_BUFFER_BIT | gl.GL_DEPTH_BUFFER_BIT)# 设置清屏颜色为白色gl.glClearColor(1.0, 1.0, 1.0, 1.0)# 使用当前相机设置激活显示上下文self.dcam.Activate(self.scam)# 绘制相机轨迹:设置线宽和颜色(绿色)gl.glLineWidth(1)gl.glColor3f(0.0, 1.0, 0.0)pangolin.DrawCameras(self.state[0])# 绘制 3D 点云:设置点大小和颜色(红色)gl.glPointSize(2)gl.glColor3f(1.0, 0.0, 0.0)pangolin.DrawPoints(self.state[1])# 完成当前帧并交换缓冲区pangolin.FinishFrame()def display(self):if self.q is None:returnposes, pts = [], []for f in self.frames:# 收集所有相机位姿poses.append(f.pose)for p in self.points:# 收集所有地图点坐标pts.append(p.pt)# 将最新位姿和点云数据放入队列,供可视化线程使用self.q.put((np.array(poses), np.array(pts)))
Map 类说明:Map类使用 Pangolin 管理并可视化一个 3D 地图。其中,frames表示相机位姿,points表示地图中的 3D 点。该类启动一个独立的查看器线程,以非阻塞方式持续更新和渲染 3D 场景。它会初始化 Pangolin 窗口,并配置相机和显示上下文以支持 3D 交互。display()方法将当前的相机位姿和地图点更新到队列中,由查看器线程读取并渲染,从而可视化相机轨迹和 3D 点云。
class Point(object):# Point 表示世界坐标系中的一个 3D 点# 每个点会被多个帧观测到def __init__(self, mapp, loc):self.frames = [] # 观测到该点的帧列表self.pt = loc # 3D 坐标位置self.idxs = [] # 对应特征点在各帧中的索引# 根据当前地图中已有点的数量,分配唯一 IDself.id = len(mapp.points)# 将该点加入地图的点列表中mapp.points.append(self)def add_observation(self, frame, idx):# frame 是 Frame 类的实例self.frames.append(frame)self.idxs.append(idx)
Point 类说明:Point类表示一个在世界坐标系中的 3D 点,可被多个帧观测到。初始化时传入位置坐标loc,并根据当前地图中已有数量分配唯一 ID,随后将自身添加到地图的点列表中。add_observation()方法用于记录该点在某一帧中的观测信息,包括对应的帧对象和特征点索引。
display.py 文件说明
最后是
display.py
import sdl2import sdl2.extimport cv2class Display(object):def __init__(self, W, H):sdl2.ext.init()self.window = sdl2.ext.Window("Tim Slam", size=(W, H))self.window.show()self.W, self.H = W, Hdef paint(self, img):img = cv2.resize(img, (self.W, self.H))# 获取 SDL2 事件列表events = sdl2.ext.get_events()for event in events:# 如果检测到窗口关闭事件,则退出程序if event.type == sdl2.SDL_QUIT:exit(0)# 获取窗口表面的像素数据(3D NumPy 数组)surf = sdl2.ext.pixels3d(self.window.get_surface())# 将调整尺寸后的图像写入窗口表面# img.swapaxes(0, 1) 用于交换数组轴,以匹配 SDL 表面的数据格式surf[:, :, 0:3] = img.swapaxes(0, 1)# 刷新窗口,显示更新后的图像self.window.refresh()
Display 类说明:Display类使用 SDL2 创建一个图像显示窗口。其paint()方法接收一张图像,将其缩放到窗口尺寸,处理窗口事件(如关闭),并将图像像素数据写入 SDL 表面。由于 SDL 表面的内存布局与 OpenCV 图像不同,需通过swapaxes(0, 1)调整数组维度。最后调用refresh()刷新窗口,实时显示图像。

我希望您已经理解了整个实现过程,以及各个步骤是如何相互关联、共同完成同步定位与建图(SLAM)的。
至此,本文已接近尾声,现在正是了解单目 SLAM 领域一项重要突破的好时机。当前已有诸如 NeRF-SLAM、高斯泼溅 SLAM(Gaussian Splatting SLAM)等新技术,但深入理解最初的算法始终能帮助你全面把握问题的本质,而在此过程中掌握的工具和思想也能广泛应用于其他领域。
ORB-SLAM 概述
ORB-SLAM 是视觉 SLAM 领域的一项重大突破。其独特之处在于,它包含了构建一个鲁棒 SLAM 系统所需的所有核心组件。ORB-SLAM 的前端与后端算法经过精心设计,在确保高精度的同时实现了实时性能。
ORB-SLAM 使用 ORB(Oriented FAST and Rotated BRIEF)算法进行特征提取,但并非所有采用 ORB 作为特征提取方法的 SLAM 系统都能被称为 ORB-SLAM。正如前文所述,许多 SLAM 实现确实使用 ORB 进行特征提取,但这并不意味着它们就是 ORB-SLAM。
以下是 ORB-SLAM 的主要贡献:

所有任务均使用 ORB 特征
:在跟踪、建图、重定位和回环检测中均采用相同的 ORB 特征,确保了系统的高效性、简洁性和可靠性。
在大型环境中实现实时运行
:通过共视图(covisibility graph)将跟踪与建图聚焦于局部共视区域,其性能不受全局地图规模的影响。
实时回环检测
:优化一种称为“本质图”(Essential Graph)的位姿图,该图由生成树、回环连接以及共视图中的强边构成。
实时相机重定位
:对视角变化和光照变化具有显著的不变性,能够在跟踪失败后恢复定位,并增强地图的可复用性。
鲁棒的初始化流程
:通过模型选择机制,自动且鲁棒地完成地图初始化,适用于平面和非平面场景。
“适者生存”的地图点与关键帧管理策略
:采用“大量生成、严格剔除”的策略,即慷慨地生成新地图点和关键帧,但严格剔除冗余项,从而提升跟踪的鲁棒性,并支持长期(lifelong)运行。
ORB-SLAM 是 SLAM 领域的一项创新性方法。但在它之前,已有多种实现对该领域作出了重要贡献。以下是各项代表性工作的发布时间线。
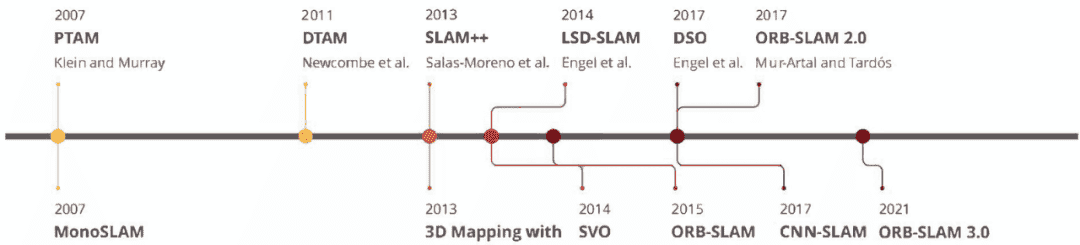
ORB-SLAM 后来又发布了两个扩展版本,分别是 ORB-SLAM 2 和 ORB-SLAM 3。
ORB-SLAM 2
支持创建和管理多个地图,并扩展了原始能力以处理 RGB-D 和单目相机的数据,从而能够在多样化的环境中实现高效的建图和重定位。
ORB-SLAM 3
则集成了惯性测量单元(IMU)数据与视觉数据,以增强鲁棒性和准确性,并支持立体相机和立体惯性相机系统,在 3D 建图和定位任务中提供了更高的通用性和精确度。
我们将在后续的文章中详细介绍所有版本的 ORB-SLAM,包括代码解析以及如何运行它们。
核心要点
SLAM 是多种不同方法的集合体,旨在创建环境的 3D 地图并估计相机位姿。这使得 SLAM 非常具有挑战性,因为任何一个环节出错都可能影响其他部分。因此,理解涉及的所有步骤非常重要。
理解坐标系、图像形成及对极几何对于掌握视觉 SLAM 算法的工作原理至关重要。了解如何使用位姿估计和三角化来估算 3D 地图点也非常重要。深入理解这些主题,如校准、图像拼接等,将会大有裨益。
Python 实现的简单单目视觉 SLAM 的代码解释,特别是
main.py
extractor.py
结论
概率 SLAM 问题的起源可以追溯到 1986 年在旧金山举行的 IEEE 机器人与自动化会议,标志着机器人技术和人工智能中概率方法的早期应用。三十多年后的今天,我们已经发展到了可学习的 SLAM 和创新技术,比如基于 LiDAR 的 SLAM、高斯泼溅 SLAM 以及 NeRF SLAM。如今,无论是波士顿动力公司的 Spot 机器人还是特斯拉的自动驾驶汽车,任何自主机器人在未知地形上导航时都依赖于 SLAM 或类似的定位技术。作为机器人工程师,理解定位或 SLAM 的工作原理是至关重要的。
随着我后续相关的SLAM文章发布,我们将深入了解更高级的主题和实现,包括 ROS2、Gazebo Sim、Carla、ORB-SLAM3、LiDAR SLAM 和目标检测,最终完成在 Carla 中构建自主车辆的最终项目。
对其他领域感兴趣的可以看这些文章
全新多视角三维重建DUSt3R的原理详解与成果展示
ADAS中基于深度学习的双目深度估计感知技术:以Stereo Transformer (STTR)模型的微调与推理为例
3D高斯泼溅(3D Gaussian Splatting)介绍--论文解析及使用以及在自定义数据集上的训练
激光雷达SLAM:同步定位与建图(slam)详细介绍


















暂无评论内容