跟我学用OFFICE（32）——卡方检验（Chitest）

044 chitest

助记：英文“chi-square test”

类别：统计

语法：

chitest(actual_range,expected_range)

参数：2个参数

• actual_range 为包含（实际）观察值的数据区域，将对期望值作检验。
• expected_range 为包含行列汇总的乘积与总计值之比率的数据区域，即期望值的区域。

说明：

• 观察值和期望值一一对应，如果actual_range和expected_range个数不同，返回#N/A错误。

• Excel 2007的协助里面还有三条说明内容，翻译的不太像中国话，在此不列出了。其中自由度的公式为df=(r-1)(c-1)，如果是单行或单列时括号内按1处理，不允许r=c=1。

用法：返回独立性检验值。

百度百科上卡方检验的基本原理很容易理解：“卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。”

1）进入chitest函数的协助，将示例复制到一个新建的空白工作表中。

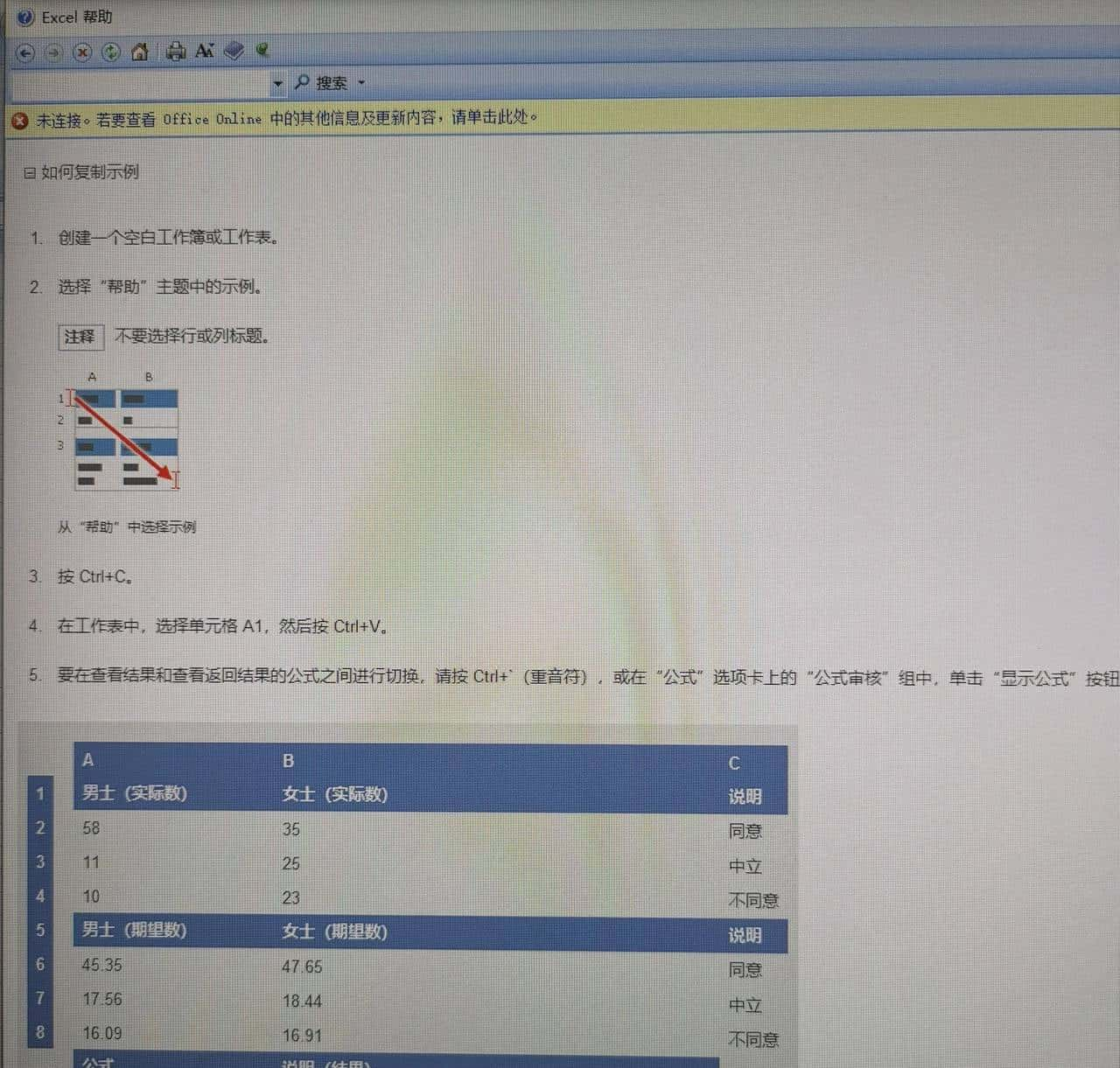
2）调整字体大小、行高、列宽。只有A10单元格是公式，其他都是人工录入的文本。实则根据参数的说明，期望数是可以使用公式计算的，即行列汇总的乘积与总计值之比率。

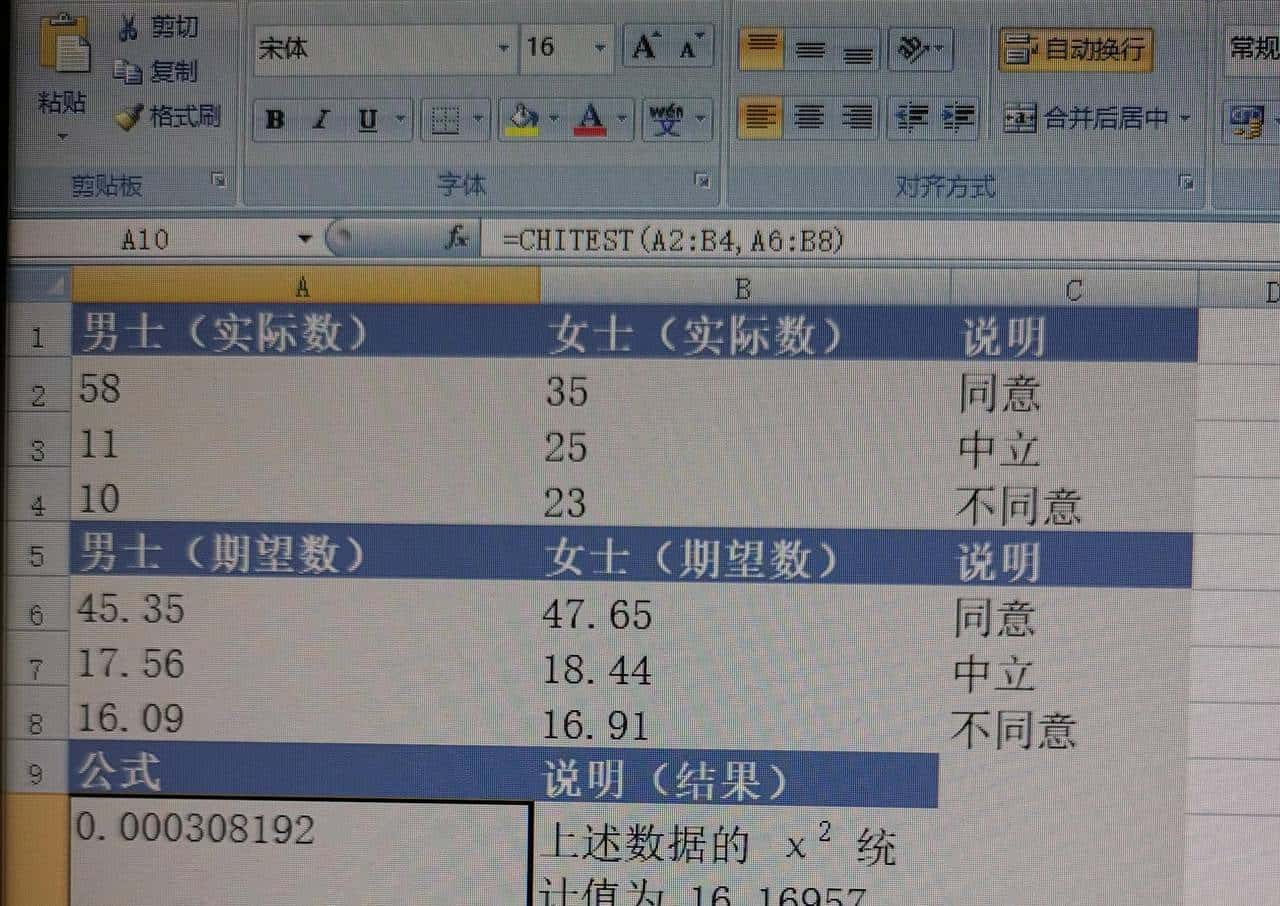
3）选择A6单元格，输入“=sum($A2:$B2)*sum(A$2:A$4)/sum($A$2:$B$4)”，利用单元格右下角的填充柄将公式填充到B8，先下后右或者先右后下均可。由于精度提高，A10的数值也改变了。

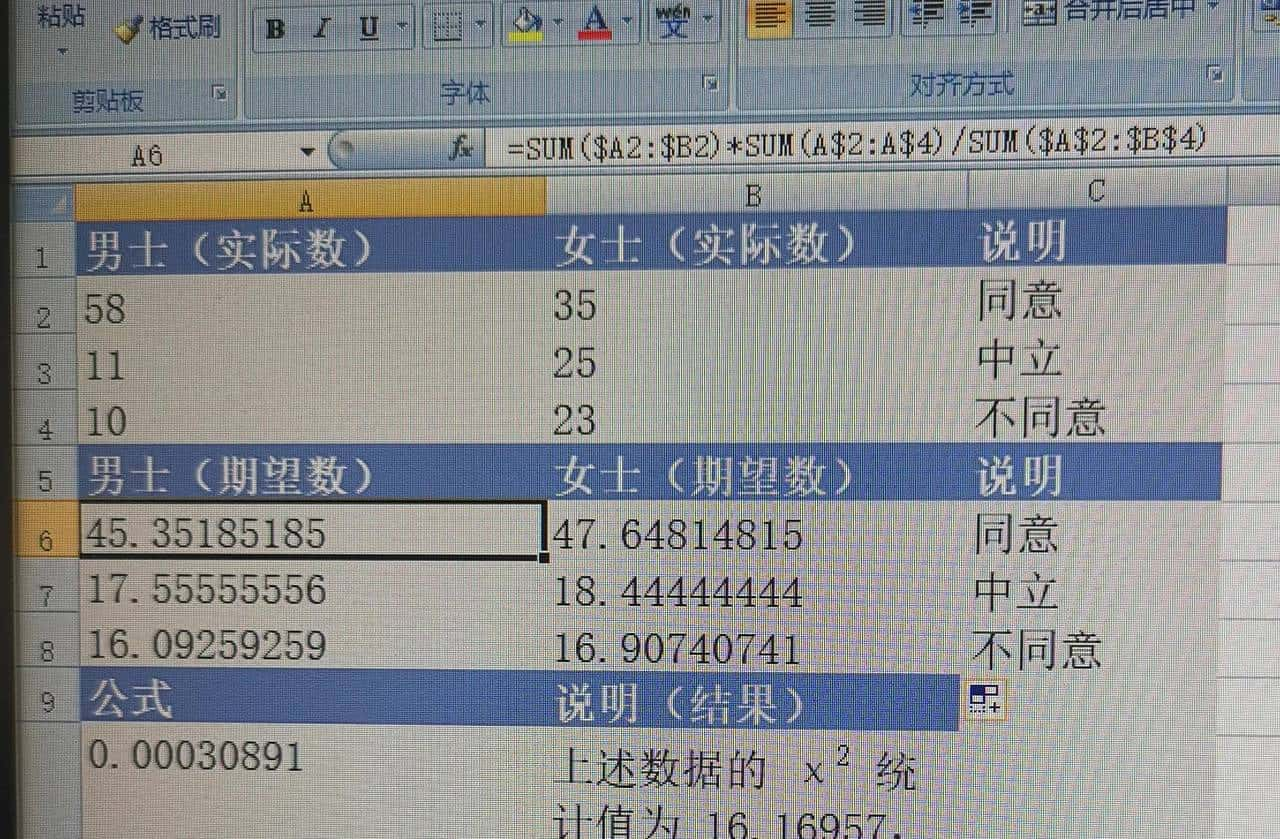
4）实际数和期望数区域的行列汇总和总计都是一样的。算式可以这样理解，总计sum($A$2:$B$4)=162是总的意见数量，3行的合计sum($A2:$B2)分别是同意（93）、中立（36）、不同意（33）的总数，两者相除便是3种意见分别占总数的比率，作为期望概率。2列合计sum($A2:$B2)分别是男（79）、女（83）的总人数，分别乘以上面得出的比率，便可以计算出男士和女士中同意、中立、不同意的期望人数，和实际数是有差异的。

5）目前我们用上面的卡方统计公式验证一下。在A11中填入“验证”，A12输入公式“=(A2-A6)^2/A6”，并填充到B14，分别计算出每一实际值与对应期望值的数值。

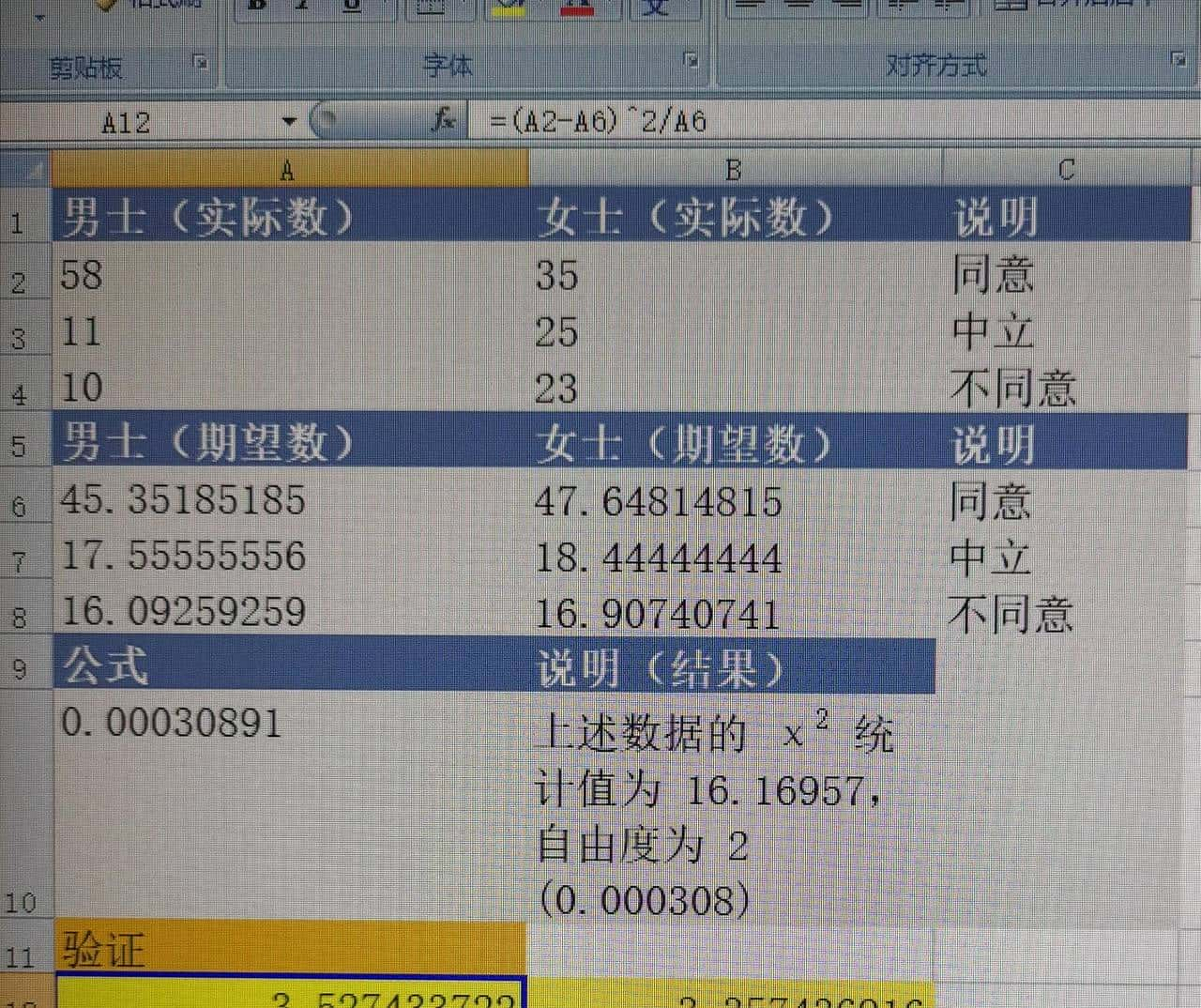
6）对A12:B14求和即为卡方统计结果。

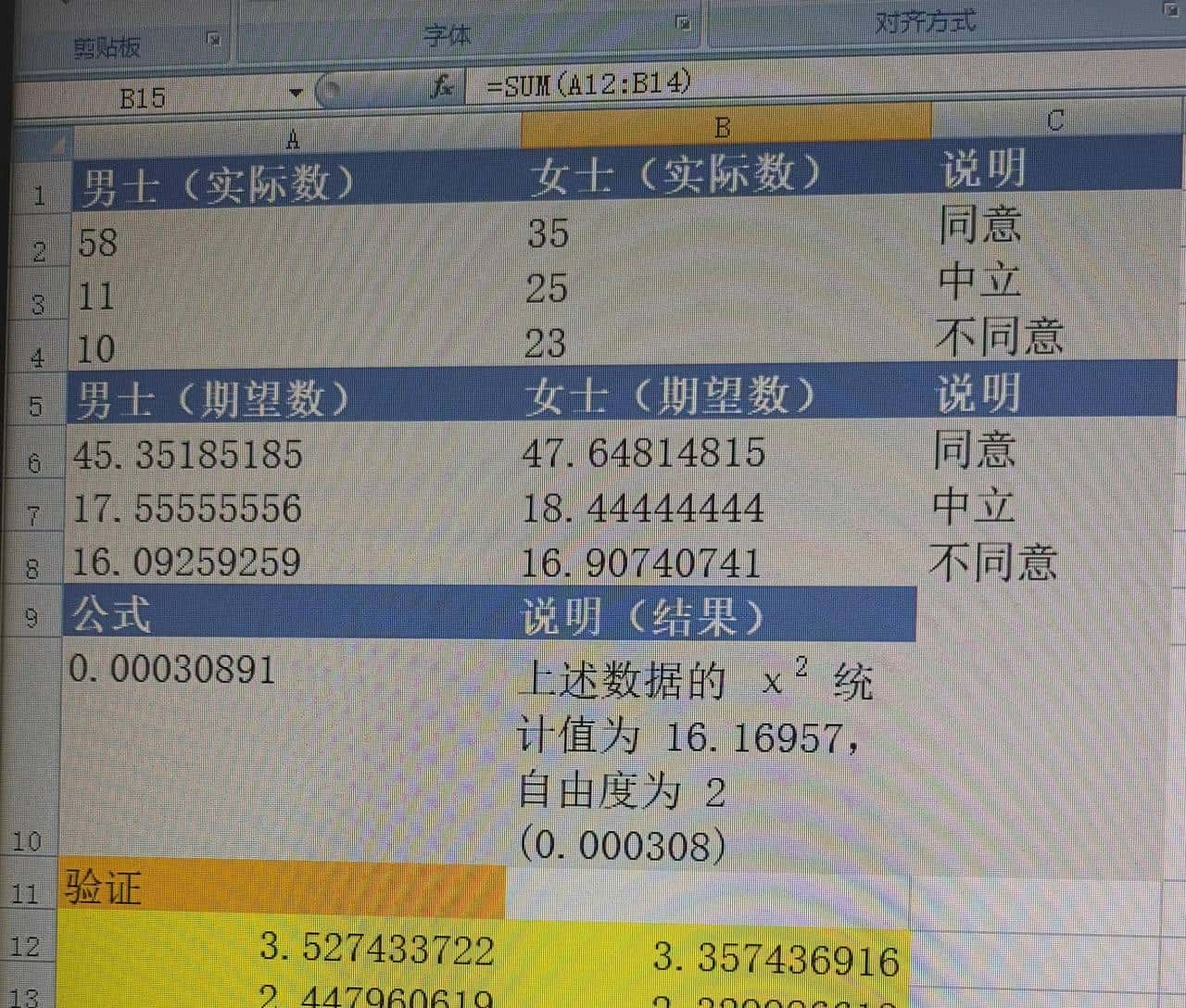
7）计算自由度输入下图的公式。

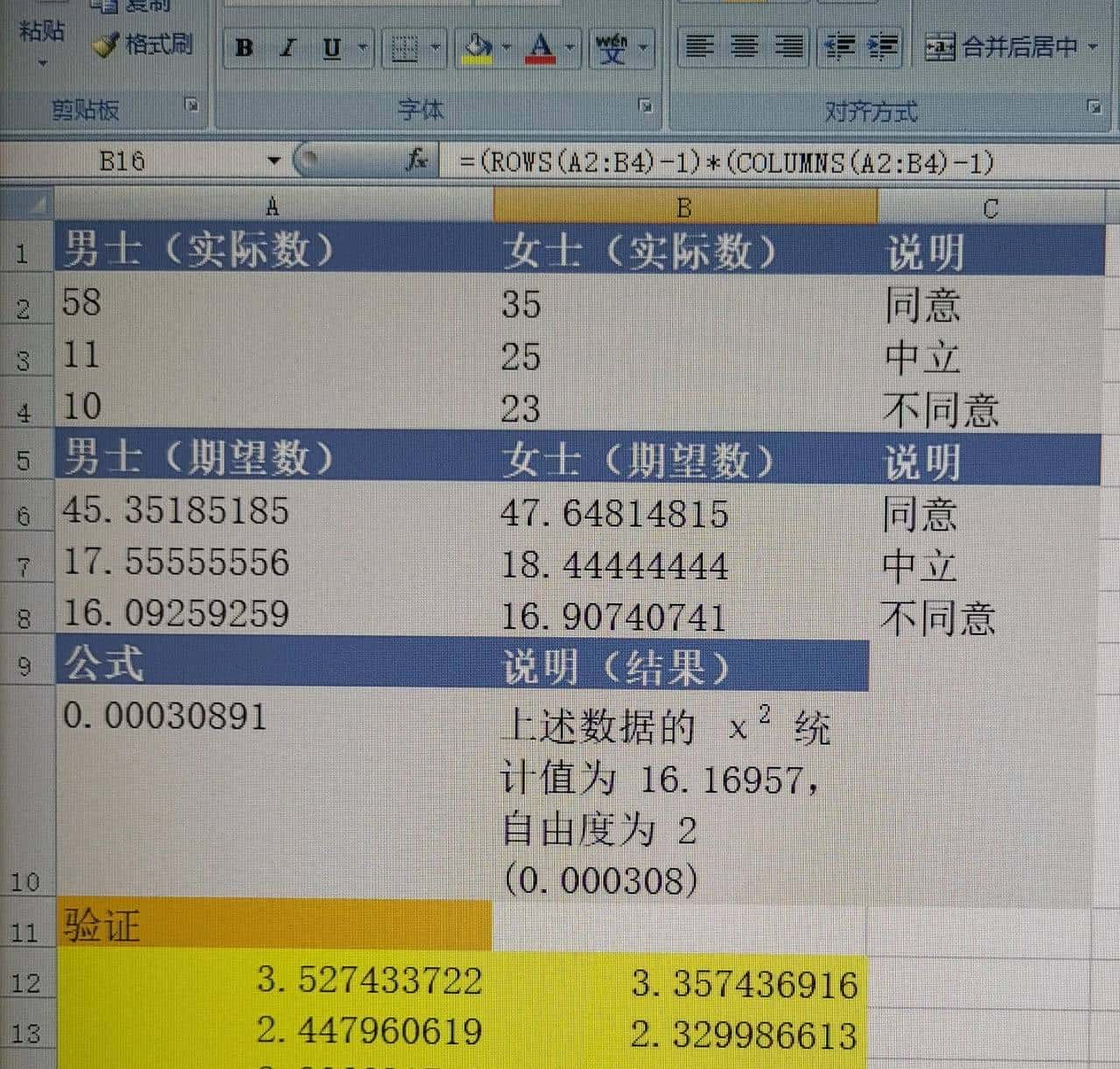
8）计算卡方分布的单尾概率。

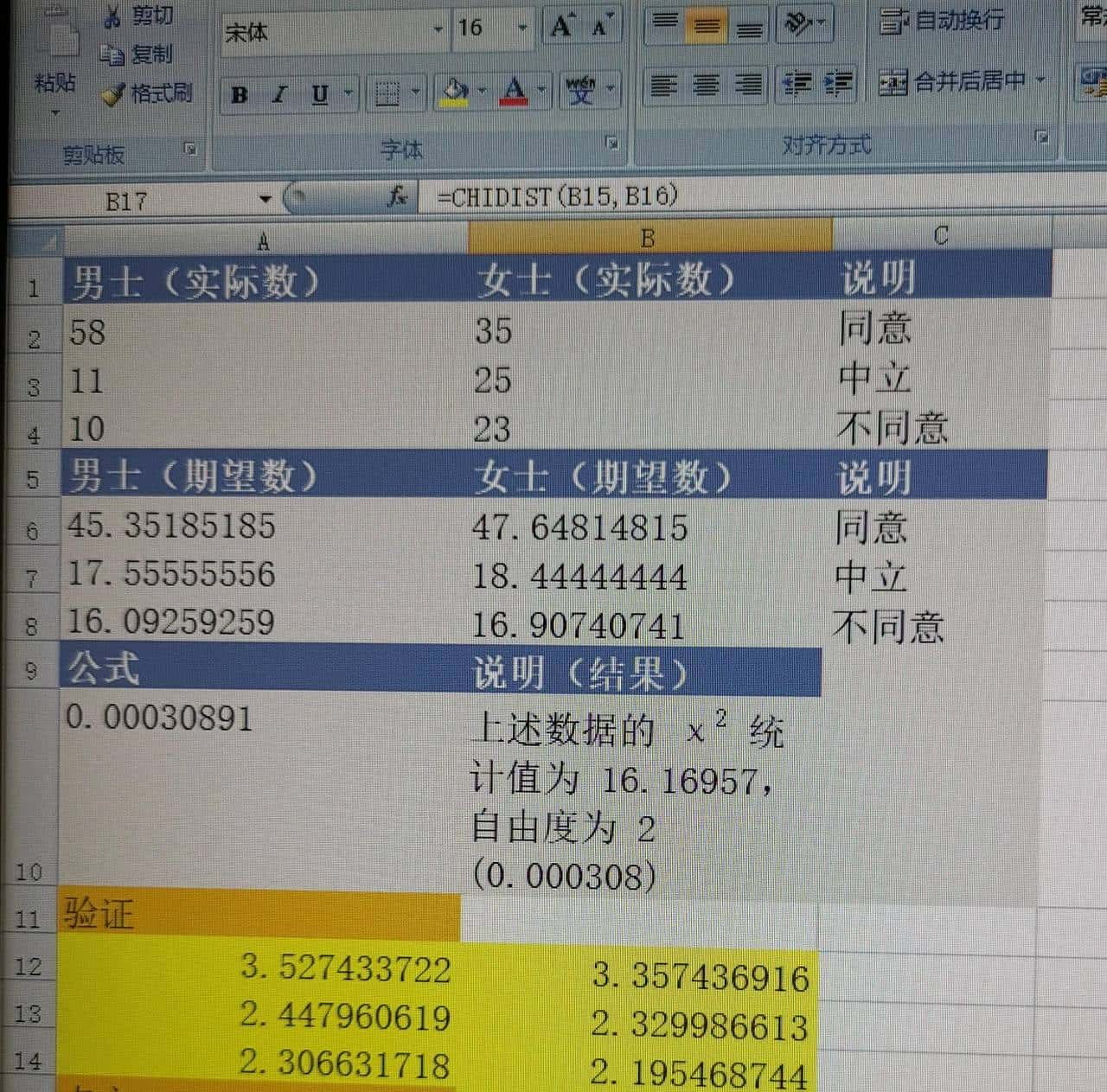
9）结果表明只有万分之三的概率接受这样的结果，数据有问题。我们把女士人数改成男士的一半，这样的结果就不受性别影响了，男女的意见一样。

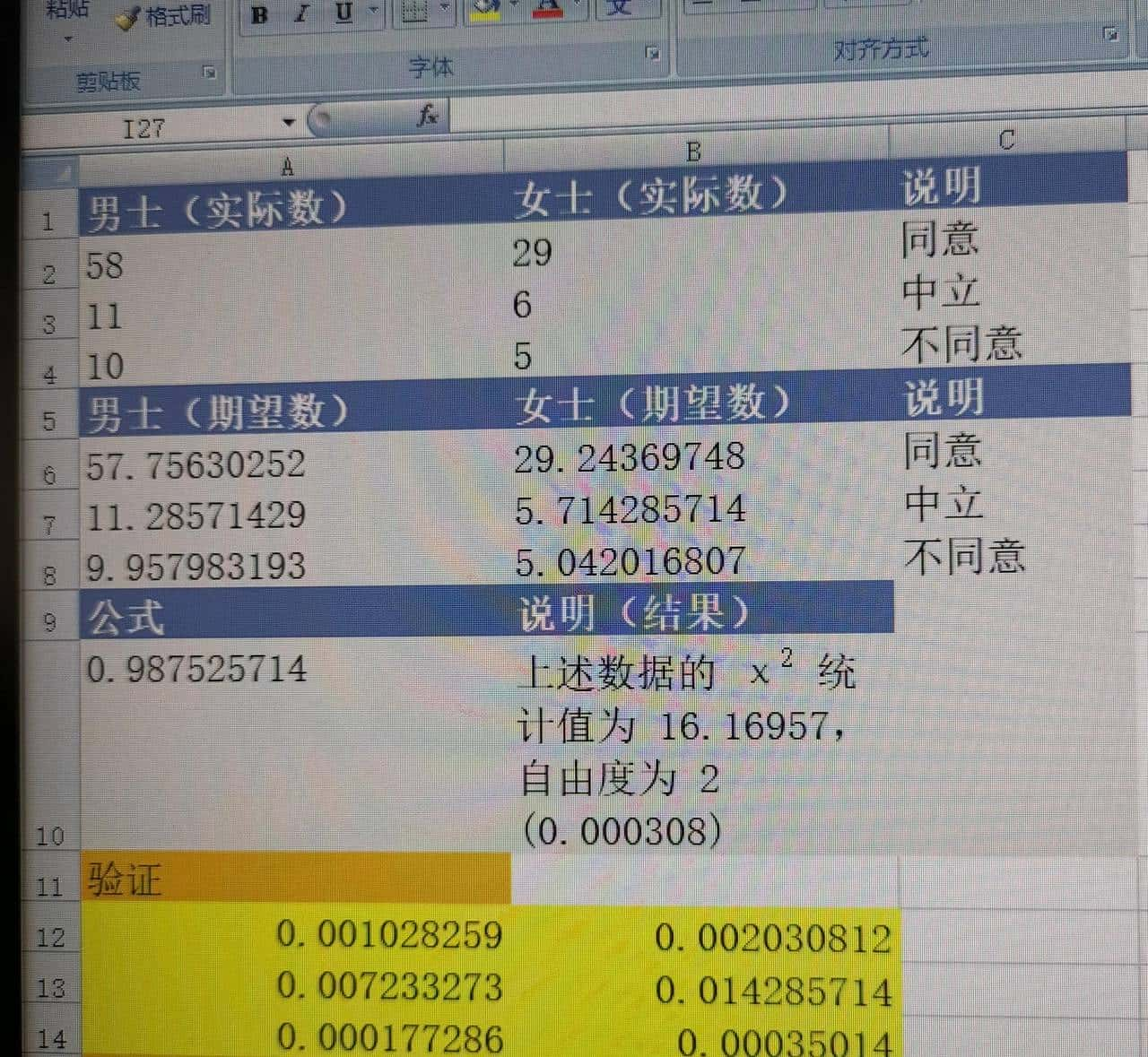
10）有些情况下期望值是已知的，列如掷骰子、抛硬币、轮盘赌等等。自行搜索一下用卡方检验判断骰子是否均匀、是否有人动手脚。

（待续）