1. 引言
无刷直流电机(BLDC)因其高功率密度、高效率等优点,在工业控制、汽车电子和家电领域得到广泛应用。磁场定向控制(FOC)作为目前最先进的BLDC电机控制技术,能够实现平滑的转矩控制和宽范围调速。本文将深入解析FOC控制的数学原理、实现方案和编程技巧,帮助工程师更好地理解和应用这一技术。
2. FOC控制基本原理
2.1 核心思想
FOC的基本思想是通过坐标变换,将三相交流量转换为旋转坐标系下的直流量,从而实现类似直流电机的控制效果。其核心目标是实现转矩与磁链的解耦控制,使得电机转矩能够快速响应且波动小。
2.2 数学基础
2.2.1 Clarke变换
将三相静止坐标系ABC转换为两相静止坐标系αβ:
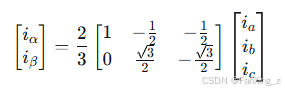
在实际应用中,常采用幅值不变变换,系数改为
2.2.2 Park变换
将两相静止坐标系αβ转换为两相旋转坐标系dq:
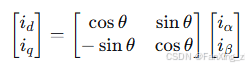
其中θ为转子电角度。
2.2.3 反Park变换
将旋转坐标系dq转换回静止坐标系αβ:

2.3 转矩与磁链方程
在dq坐标系下,电磁转矩方程为:
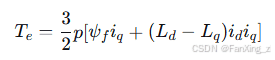
对于表贴式永磁同步电机(SPMSM),
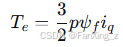
这表明通过控制
3. FOC系统架构与实现方案
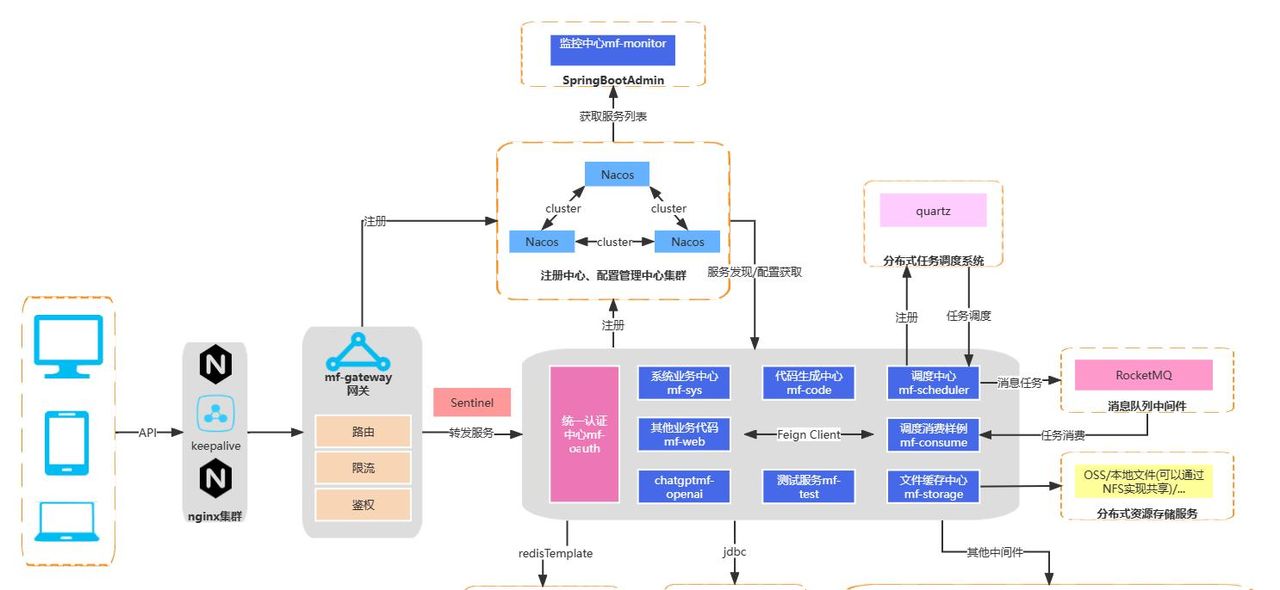
3.1 系统整体架构
完整的FOC控制系统包含以下模块:
下载
电流采样 → Clarke变换 → Park变换 → PI控制器 → 反Park变换 → SVPWM → 逆变器
↑ |
| ↓
位置/速度反馈 ←------------ 位置/速度估计 ←----------------- 电机
3.2 关键模块实现
3.2.1 电流采样与处理
三相电流采样通常只需两相(


// 电流采样处理示例代码
void ADC_Handler(void) {
// 读取ADC值
int32_t adc_a = ADC_GetValue(ADC_CH_A);
int32_t adc_b = ADC_GetValue(ADC_CH_B);
// 转换为实际电流值(考虑偏移和增益)
current_a = (adc_a - offset_a) * gain_a;
current_b = (adc_b - offset_b) * gain_b;
current_c = -current_a - current_b;
// 应用低通滤波
current_a_filt = LPF_Apply(&lpf_a, current_a);
current_b_filt = LPF_Apply(&lpf_b, current_b);
}3.2.2 位置/速度检测
编码器方案:
增量式编码器:通过ABZ脉冲计算位置和速度
绝对式编码器:直接读取绝对位置
无传感器方案:
滑模观测器(SMO)
模型参考自适应系统(MRAS)
高频注入法(适用于零低速)
位置估算算法示例:
// 基于反电动势的位置估算简化代码
void EstimatePosition(void) {
// 计算反电动势
float emf_alpha = v_alpha - R * i_alpha - L * di_alpha_dt;
float emf_beta = v_beta - R * i_beta - L * di_beta_dt;
// 估算电角度
estimated_angle = atan2(-emf_alpha, emf_beta);
// 估算电速度
estimated_speed = (estimated_angle - last_angle) / delta_t;
last_angle = estimated_angle;
}3.2.3 PI控制器设计
dq轴电流环PI参数设计基于电机数学模型:
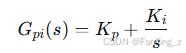
其中:

//抗饱和PI控制器实现typedefstructfloatKp;floatKi;floatintegral;floatoutputlimit;floatintegrallimit;PIController;floatPIUpdate(PIController∗pi,floaterror,floatdt)//比例项floatproportional=pi−>Kp∗error;//积分项(带抗饱和)pi−>integral+=pi−>Ki∗error∗dt;//积分限幅if(pi−>integral>pi−>integrallimit)pi−>integral=pi−>integrallimit;elseif(pi−>integral<−pi−>integrallimit)pi−>integral=−pi−>integrallimit;//计算输出floatoutput=proportional+pi−>integral;//输出限幅if(output>pi−>outputlimit)output=pi−>outputlimit;elseif(output<−pi−>outputlimit)output=−pi−>outputlimit;returnoutput;” role=”presentation”>//抗饱和PI控制器实现typedefstructfloatKp;floatKi;floatintegral;floatoutputlimit;floatintegrallimit;PIController;floatPIUpdate(PIController∗pi,floaterror,floatdt)//比例项floatproportional=pi−>Kp∗error;//积分项(带抗饱和)pi−>integral+=pi−>Ki∗error∗dt;//积分限幅if(pi−>integral>pi−>integrallimit)pi−>integral=pi−>integrallimit;elseif(pi−>integral<−pi−>integrallimit)pi−>integral=−pi−>integrallimit;//计算输出floatoutput=proportional+pi−>integral;//输出限幅if(output>pi−>outputlimit)output=pi−>outputlimit;elseif(output<−pi−>outputlimit)output=−pi−>outputlimit;returnoutput;//抗饱和PI控制器实现typedefstructfloatKp;floatKi;floatintegral;floatoutputlimit;floatintegrallimit;PIController;floatPIUpdate(PIController∗pi,floaterror,floatdt)//比例项floatproportional=pi−>Kp∗error;//积分项(带抗饱和)pi−>integral+=pi−>Ki∗error∗dt;//积分限幅if(pi−>integral>pi−>integrallimit)pi−>integral=pi−>integrallimit;elseif(pi−>integral<−pi−>integrallimit)pi−>integral=−pi−>integrallimit;//计算输出floatoutput=proportional+pi−>integral;//输出限幅if(output>pi−>outputlimit)output=pi−>outputlimit;elseif(output<−pi−>outputlimit)output=−pi−>outputlimit;returnoutput;
3.2.4 SVPWM实现
空间矢量脉宽调制通过基本电压矢量的合成,实现圆形旋转磁场。六步换相中的6个非零矢量和2个零矢量组成:

SVPWM算法步骤:
扇区判断
矢量作用时间计算
PWM占空比计算
// SVPWM扇区判断和占空比计算
void SVPWM_Calculate(float v_alpha, float v_beta, float* duty_cycles) {
// 扇区判断
float v_ref1 = v_beta;
float v_ref2 = sqrt3 * v_alpha - v_beta;
float v_ref3 = -sqrt3 * v_alpha - v_beta;
int sector = 0;
if (v_ref1 > 0) sector |= 1;
if (v_ref2 > 0) sector |= 2;
if (v_ref3 > 0) sector |= 4;
// 根据不同扇区计算占空比
switch(sector) {
case 1: // 扇区I
// 计算Tx, Ty
float T1 = v_alpha - v_beta / sqrt3;
float T2 = 2 * v_beta / sqrt3;
// 计算三相占空比
duty_cycles[0] = (1 - T1 - T2) * 0.5;
duty_cycles[1] = duty_cycles[0] + T1;
duty_cycles[2] = duty_cycles[1] + T2;
break;
// 其他扇区类似...
}
}4. 编程技巧与优化
4.1 定点数运算优化
在资源受限的微控制器中,定点数运算比浮点数更高效:
// 定点数Clarke变换(Q15格式)
void Clarke_Transform_Q15(int16_t ia, int16_t ib, int16_t* ialpha, int16_t* ibeta) {
// 系数: 1/sqrt(3) ≈ 0.57735 ≈ 18918 in Q15
const int16_t ONE_BY_SQRT3 = 18918;
*ialpha = ia; // i_alpha = i_a
// i_beta = (i_a + 2*i_b) / sqrt(3)
int32_t temp = (int32_t)ia + 2 * (int32_t)ib;
*ibeta = (int16_t)((temp * ONE_BY_SQRT3) >> 15);
}4.2 查表法优化三角函数
// 预先计算sin/cos表
const int16_t sin_table[256] = {0, 804, 1608, ...};
const int16_t cos_table[256] = {32767, 32758, 32731, ...};
// 快速Park变换使用查表法
void Park_Transform_Fast(int16_t ialpha, int16_t ibeta, uint8_t angle,
int16_t* id, int16_t* iq) {
int16_t cos_val = cos_table[angle];
int16_t sin_val = sin_table[angle];
// i_d = i_alpha * cosθ + i_beta * sinθ
*id = (int16_t)(((int32_t)ialpha * cos_val + (int32_t)ibeta * sin_val) >> 15);
// i_q = -i_alpha * sinθ + i_beta * cosθ
*iq = (int16_t)((-(int32_t)ialpha * sin_val + (int32_t)ibeta * cos_val) >> 15);
}4.3 中断服务例程优化
FOC控制循环通常在PWM定时器中断中执行,优化中断服务例程至关重要:
// 优化后的FOC中断服务例程
void PWM_IRQHandler(void) {
// 清除中断标志
PWM_ClearIRQ();
// 1. 读取电流和位置
ReadCurrents();
ReadPosition();
// 2. 坐标变换
Clarke_Transform(current_a, current_b, &i_alpha, &i_beta);
Park_Transform(i_alpha, i_beta, rotor_angle, &i_d, &i_q);
// 3. PI控制
v_d_ref = PI_Update(&pi_d, i_d_ref - i_d, Ts);
v_q_ref = PI_Update(&pi_q, i_q_ref - i_q, Ts);
// 4. 反坐标变换
InvPark_Transform(v_d_ref, v_q_ref, rotor_angle, &v_alpha_ref, &v_beta_ref);
// 5. SVPWM生成
SVPWM_Generate(v_alpha_ref, v_beta_ref, duties);
// 6. 更新PWM占空比
UpdatePWM_Duty(duties);
}4.4 参数自整定技巧
// 基于继电器反馈的PI参数自整定
void AutoTune_PI(PI_Controller* pi, Motor* motor) {
// 施加小幅值方波激励
float test_signal = (tick_count % 1000 < 500) ? 0.1 : -0.1;
// 测量输出响应,计算临界增益和周期
// 根据Ziegler-Nichols法则计算PI参数
pi->Kp = 0.45 * K_critical; // K_critical为临界增益
pi->Ki = pi->Kp / (0.83 * T_critical); // T_critical为临界周期
}
5. 调试技巧与常见问题
5.1 调试步骤
开环调试:验证基本功能,确保电机旋转
电流环调试:先调d轴,再调q轴
速度环调试:在电流环稳定基础上进行
位置环调试:最后调试位置控制性能
5.2 常见问题及解决方案
问题1:电机振动或噪声大
原因:PI参数不匹配,电流采样不准
解决:重新校准电流偏移,调整PI参数
问题2:高速运行不稳定
原因:反电动势估算误差,延迟补偿不足
解决:增加前馈补偿,优化观测器带宽
问题3:启动困难
原因:初始位置检测不准,启动电流不足
解决:改进初始位置检测算法,调整启动参数
6. 结论
FOC控制技术为BLDC电机提供了高性能的控制方案,通过精确的磁场定向实现平滑的转矩控制。本文从数学原理到实际实现,详细解析了FOC系统的各个模块,并提供了实用的编程技巧和优化方法。在实际应用中,需要根据具体电机特性和应用需求,仔细调整控制参数,才能充分发挥FOC控制的优势。
随着处理器性能的提升和算法优化,FOC技术在未来的电机控制领域将展现更大的应用潜力,特别是在需要高精度、高效率和高动态响应的应用场景中。
本文涉及的理论和代码示例仅供参考,实际应用请根据具体硬件平台和电机参数进行调整。欢迎在评论区交流讨论!





















暂无评论内容