傅里叶变换是频谱方向的幺正变换;
拉普拉斯变换是带收敛权重的傅里叶变换,专攻初值问题;
幺正变换是最广义的正交旋转,傅里叶变换只是它的一个具体化身。
下面用一张“三维坐标系”来同时安放傅里叶变换(FT)、拉普拉斯变换(LT)和幺正变换(UT):
x 轴:定义域(时间/频率/复平面/希尔伯特空间)
y 轴:目标(解方程 / 压缩信息 / 改变表象 / 量子演化)
z 轴:数学结构(积分核、谱分解、群表明)
把三条轴上的关键坐标写出来,区别与联系就一目了然。
1. 傅里叶变换(FT)
数学定义
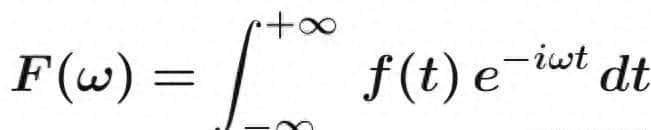
F(ω)=∫{-∞}^{+∞} f(t) e^{-iωt} dt
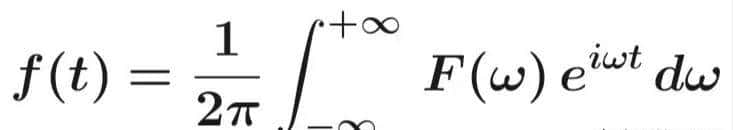
f(t)=1/(2π) ∫{-∞}^{+∞} F(ω) e^{iωt} dω
几何本质
把 L²(ℝ) 上函数分解到平面波基底 {e^{iωt}};这是 连续谱的幺正对角化。
FT 本身是幺正算子(Plancherel 定理:‖f‖₂ = ‖F‖₂)。
主要用途
微分 → 乘法:d/dt → iω,常系数 ODE/PDE 变代数方程。
频谱分析、信号压缩(JPEG、MP3)。
量子力学:动量表象 ↔ 坐标表象的 幺正变换(x̂ ↔ p̂ 的对偶空间旋转)。
局限
只能处理 t ∈ (-∞,∞);
不直接给出指数增长信号;
初值问题需人工引入边界条件。
2. 拉普拉斯变换(LT)
数学定义(单边)
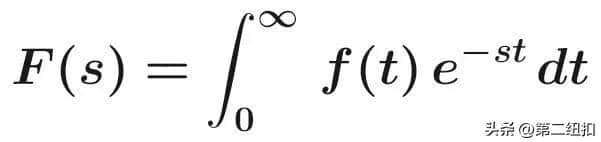
s=σ+iω ∈ ℂ
几何本质
把函数空间 L¹_loc(ℝ₊) 嵌入 Hardy 空间;
核 e^{-st} 含衰减因子 e^{-σt},因此 自动消化指数增长,把微分算子 s 化。
主要用途
初值问题一步到位:Ly′+Ry = E(t) → (Ls+R)Y(s)=E(s)+Ly(0)。
控制理论:传递函数 G(s)=Y(s)/U(s);极点分析稳定性。
电路、机械系统的瞬态响应。
与 FT 的关系
LT 沿虚轴 s=iω 退化为 FT(要求 f 指数衰减);
LT 是 FT 的解析延拓 + 加权版本;
FT 是纯虚轴上的 LT 截面。
3. 幺正变换(UT)
数学定义
U: ℋ → ℋ,满足 U†U = UU† = I(保内积、保范数)。
谱定理:任何幺正算子可写成 U = ∫{0}^{2π} e^{iθ} dE_θ,其中 {E_θ} 是谱族。
几何本质
希尔伯特空间中的刚性旋转;不改变向量长度,只改变基底。
典型实例
量子力学:时间演化 U(t)=e^{-iHt/ħ}(薛定绘景)。
量子计算:单比特门 X,Y,Z, Hadamard, 相位门都是 2×2 幺正矩阵。
傅里叶变换:FT 在 L²(ℝ) 上是幺正算子(可视为连续谱极限的 DFT)。
正交基旋转:如坐标旋转矩阵、离散余弦变换(JPEG)。
与 FT/LT 的联系
FT 本身就是连续谱极限下的幺正变换;
DFT 的 N×N 矩阵是有限维幺正矩阵(除 1/√N 归一化因子);
LT 不幺正(改变范数:∫|f|² ≠ ∫|F|²),但可视为加权希尔伯特空间上的有界算子。
4. 一张对照表
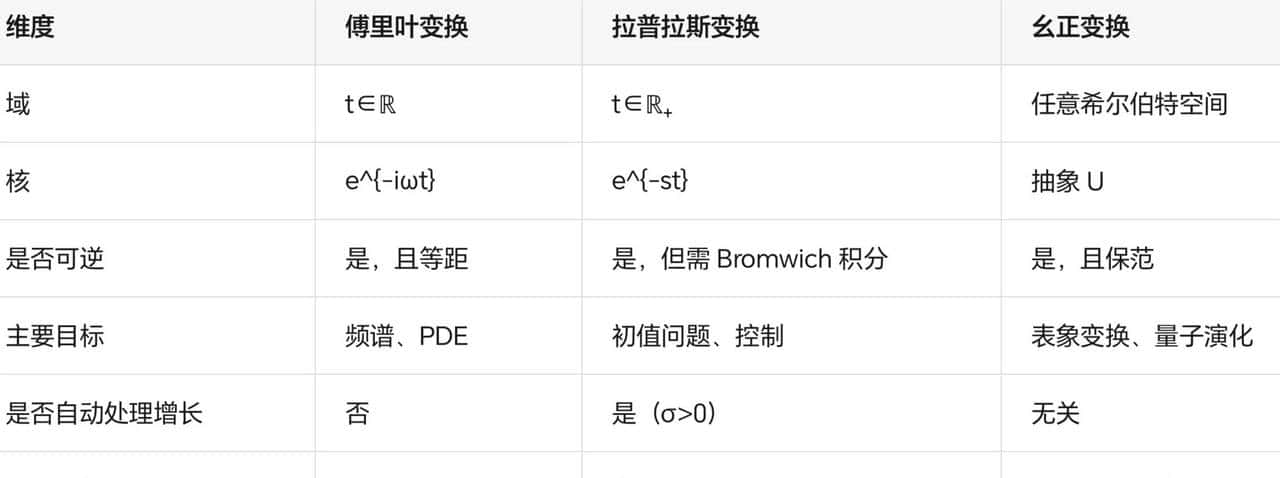



















- 最新
- 最热
只看作者