线性回归1

线性回归算法是解决监督式学习中回归问题的重大算法。它是模型假设为线性模型的经验损失最小化算法。在许多实际问题中，对象的特征与其标签之间存在着必定的关系。如果特征与标签之间的关系是近似线性的，就可以用一个线性模型来拟合这种关系。

例子1：简单线性回归

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1)
# x = -10 + 20 * np.random.rand(30)
x = np.random.uniform(-10, 10, 30)
y = 2 * x + 5 + np.random.normal(0, 0.3, 30)
plt.scatter(x, y)
# 导入sklearn，该包需要先下载安装
from sklearn.linear_model import LinearRegression

model = LinearRegression(fit_intercept=True)
model.fit(x.reshape(-1, 1), y)
xfit = np.linspace(-10, 10, 201)
yfit = model.predict(xfit.reshape(-1, 1))
plt.plot(xfit, yfit)
plt.xticks(np.arange(-15, 15, 5))
plt.yticks(np.arange(-30, 30, 5))
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.spines['left'].set_position(('data', 0))
ax.spines['bottom'].set_position(('data', 0))

plt.show()
print(f"直线的系数：{model.coef_[0]:6.2f}")
print(f"直线的截距：{model.intercept_:6.2f}")

运行结果：直线的系数： 1.99

直线的截距： 4.97

上述代码的线性回归结果

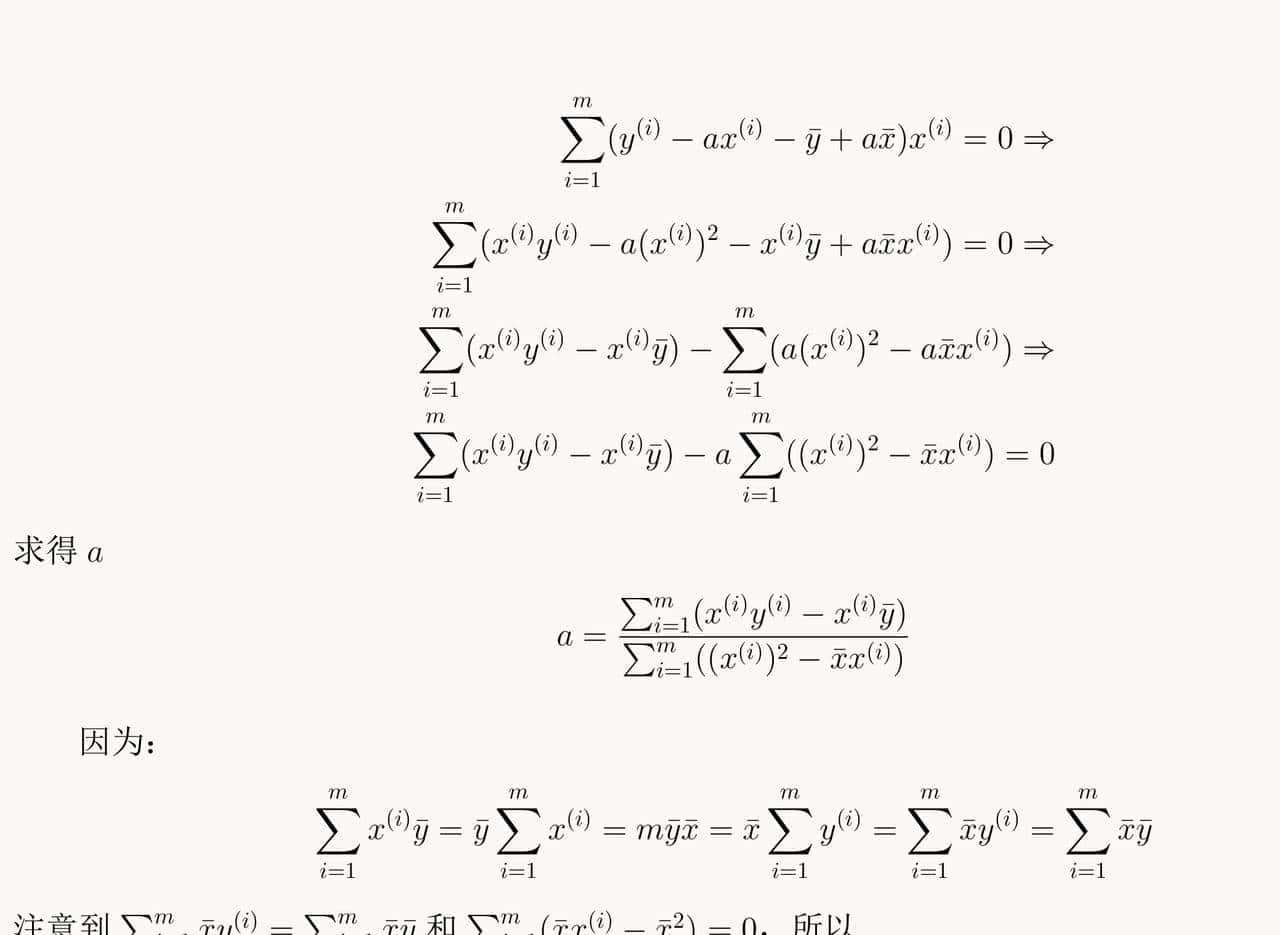
利用上述计算得到的参数，验证其与Sklearn提供的线性回归算法计算的结果的一致性。

import numpy as np
np.random.seed(1)
# x = 10 * np.random.rand(10)
# y = 2 * x + 5 + np.random.normal(0, 0.3, 10)
x = np.random.uniform(-10, 10, 30)
y = 2 * x + 5 + np.random.normal(0, 0.3, 30)
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
    num += (x_i - x_mean) * (y_i - y_mean)
    d += (x_i - x_mean) ** 2
a = num / d
b = y_mean - a * x_mean
print(f"a={a:6.2f}")
print(f"b={b:6.2f}")

运行结果：

a= 1.99

b= 4.97

斜率和截距与sklearn的结果是一致的。

(注：头条的公式编辑器实在太差了，latex公式要先转换为图片，速度超级慢，直接截图了。