Auto-Encoder是自监督方法的一种
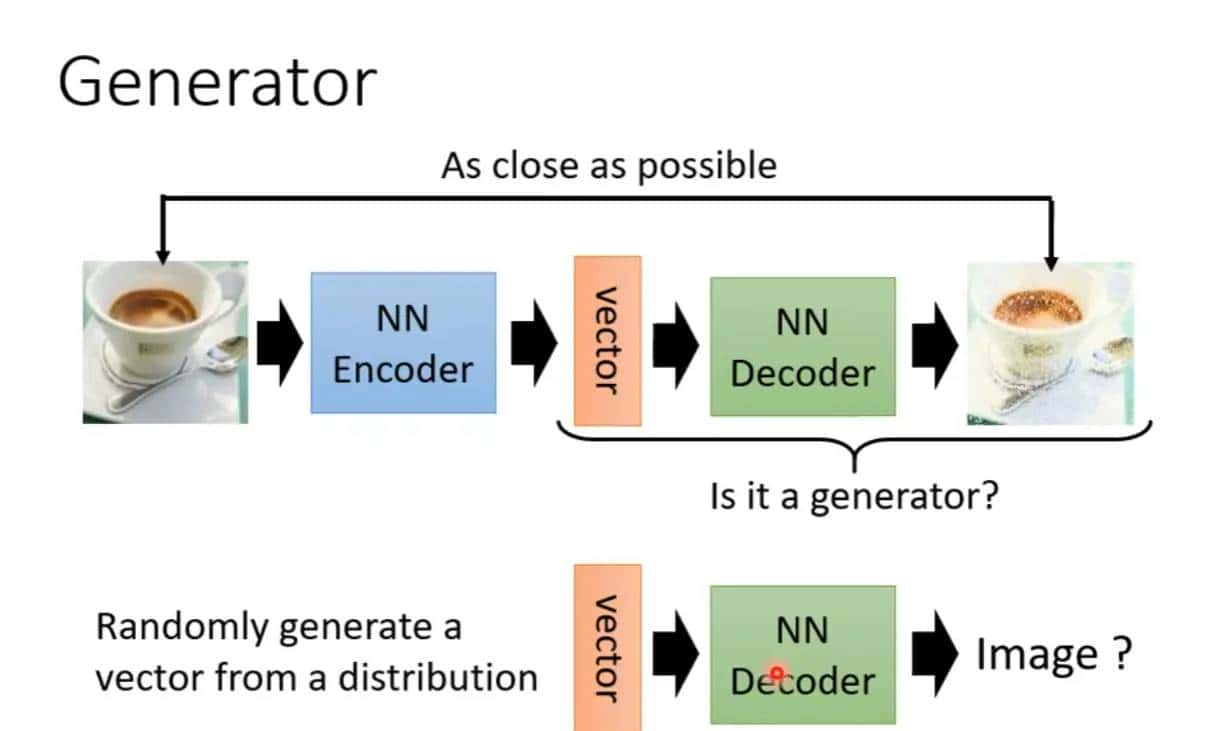
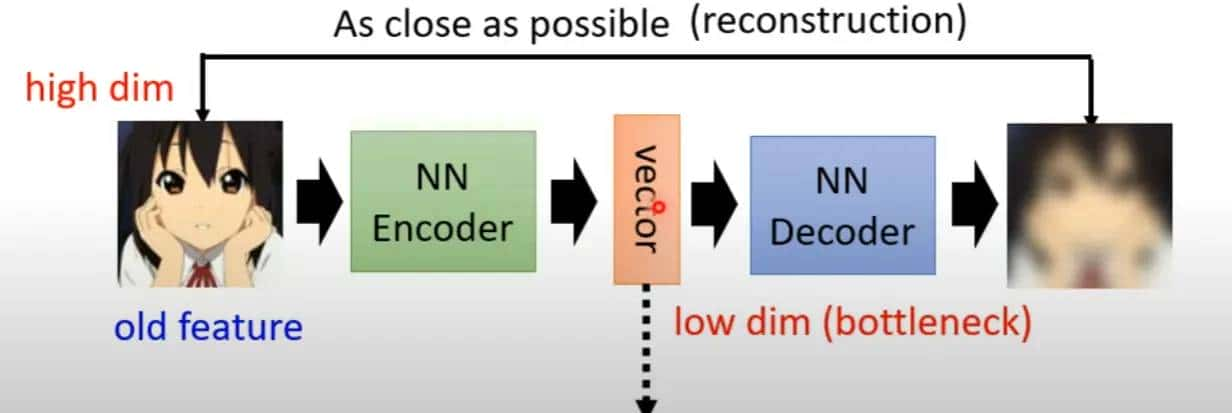
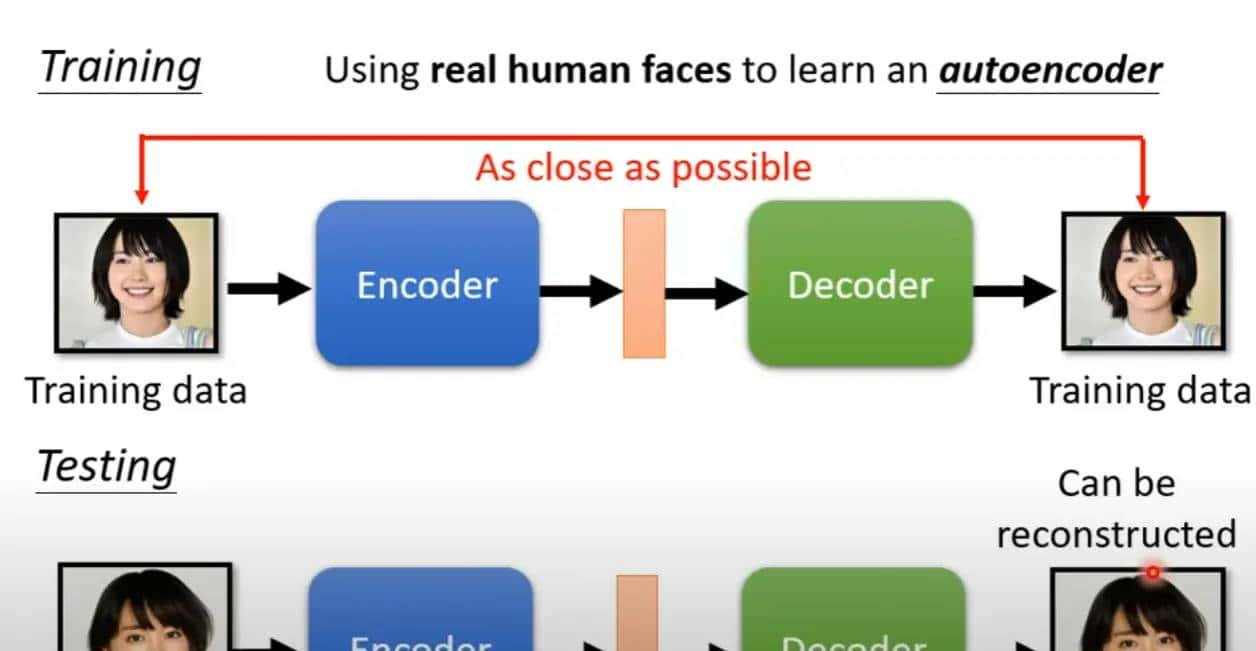
所谓自编码器实则就是通过编码器将原本高维的数据压缩为低维(bottleneck),然后解码器通过“努力”还原原来的数据,本质上就是降维的过程,和PCA,tSNE,UMAP很类似。
自监督意味着不需要任何标注资料,只需要收集到大量数据就可以做这个事情
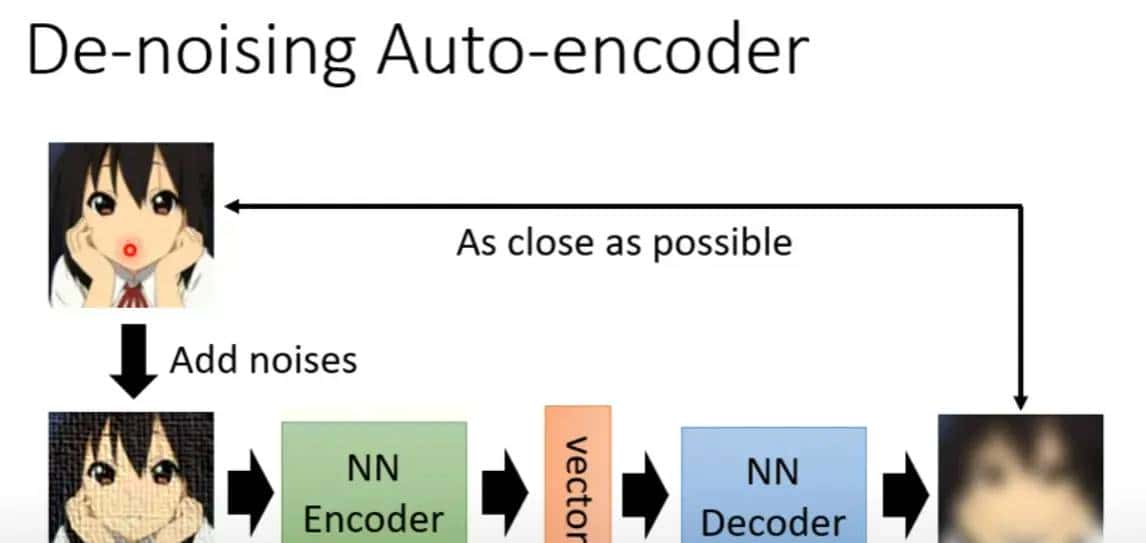
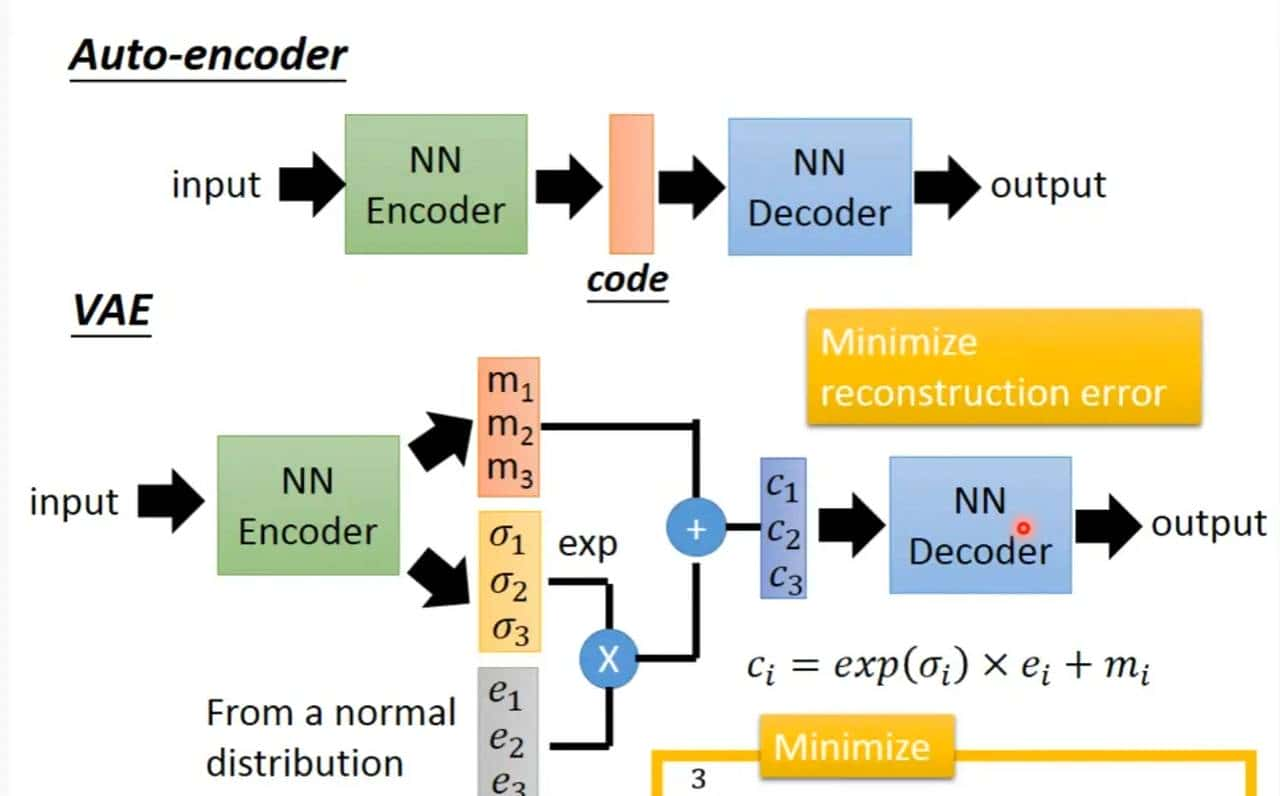
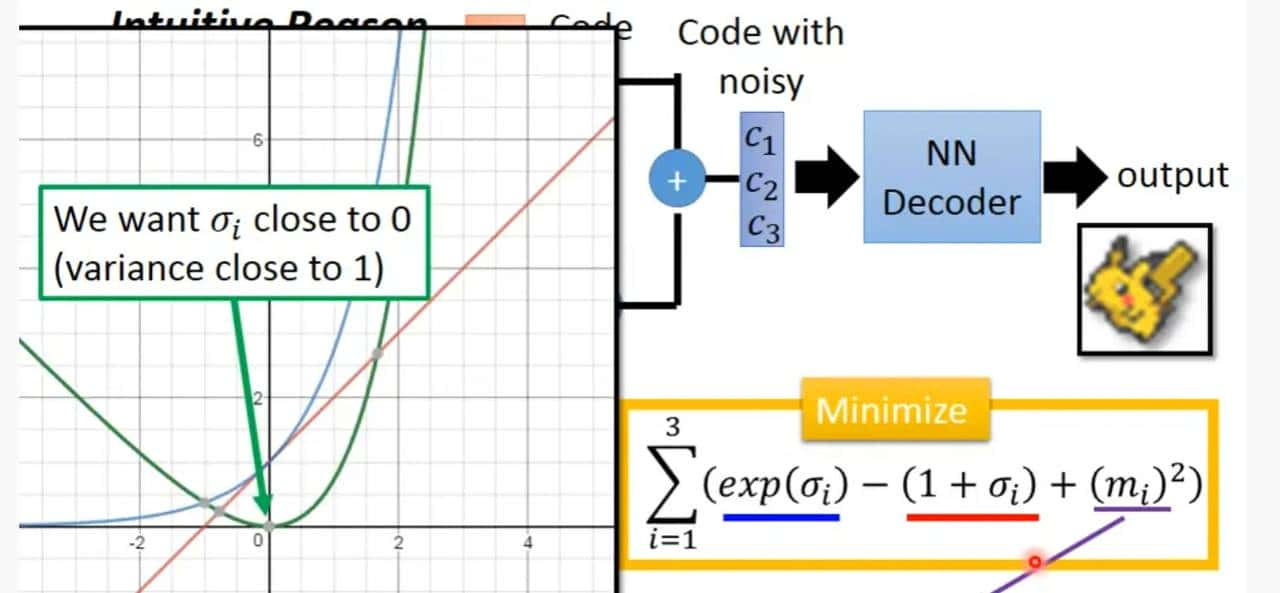
自编码器有若干种变体,这是其中一种:加入噪声的自编码器
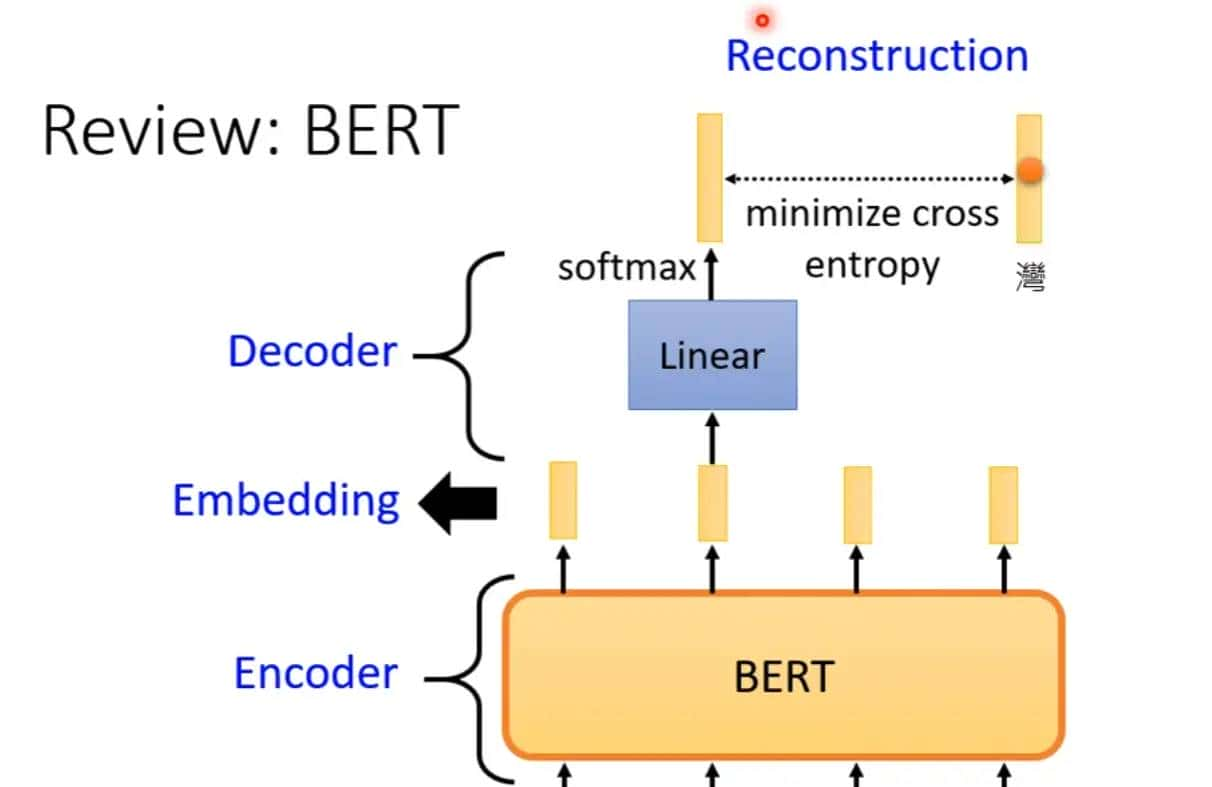
BERT原理上也可以算一种自编码器,实则就是编码然后努力还原解码
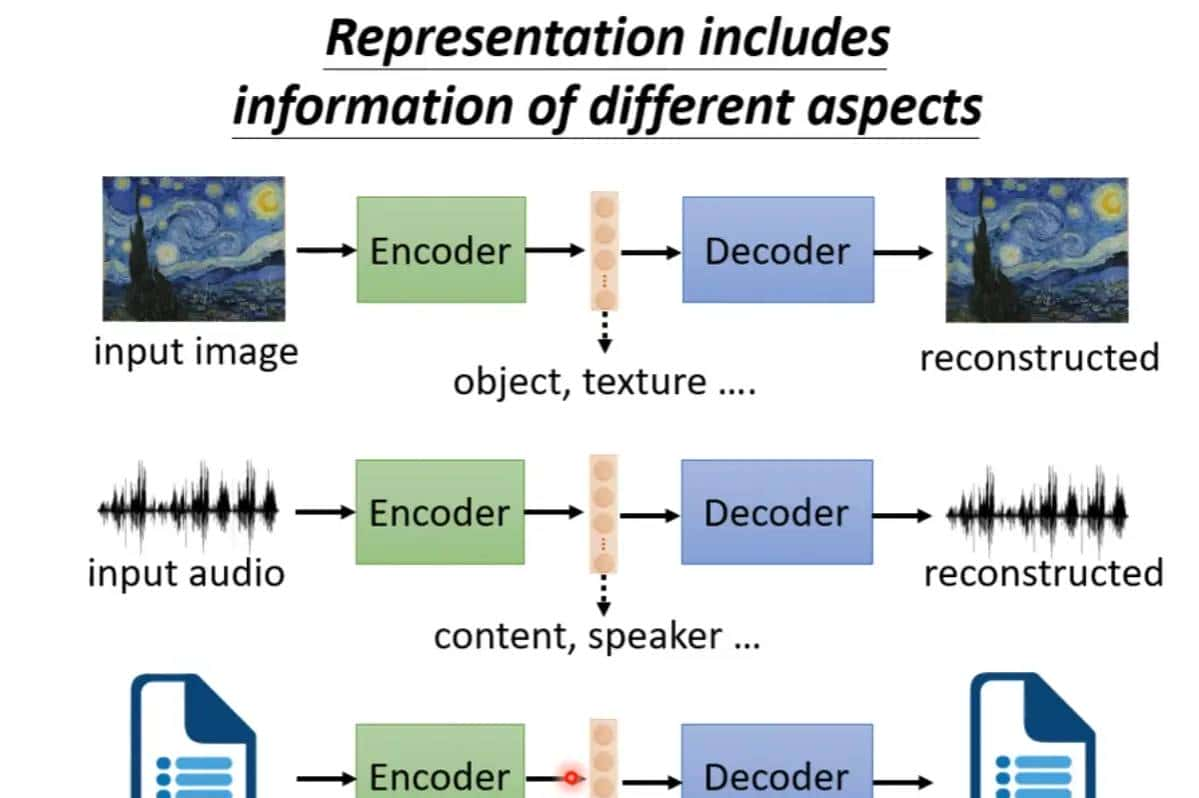
经过编码再解码的过程,那么低维潜在空间的向量便会包含输入的数据的信息,列如声音的话经过自编码的过程,中间的向量就能够包含说话的人以及说话的声音这种资讯,又列如文章就可能包含文章的内容和文章的语法
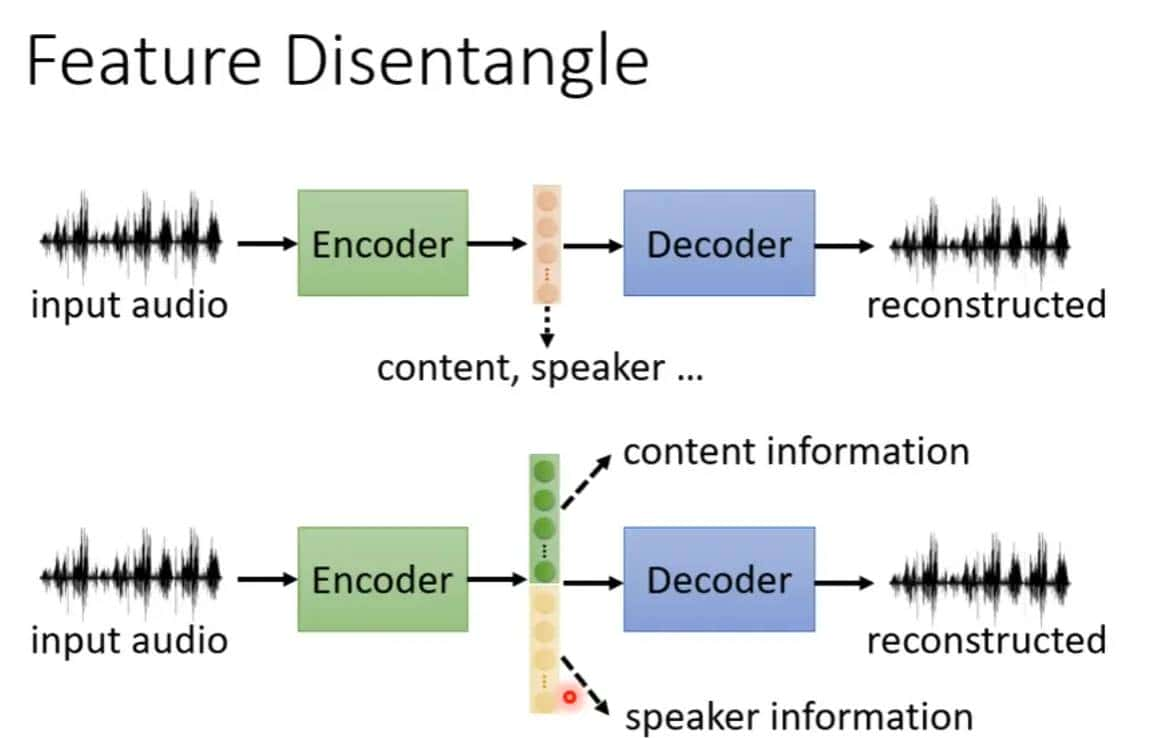
正如前面所说的,由于中间这个向量空间能够降维嵌入信息,那么我们便想知道哪些向量代表着哪些信息?列如前五十维代表着某些特征。这就是Feature Disentangle。
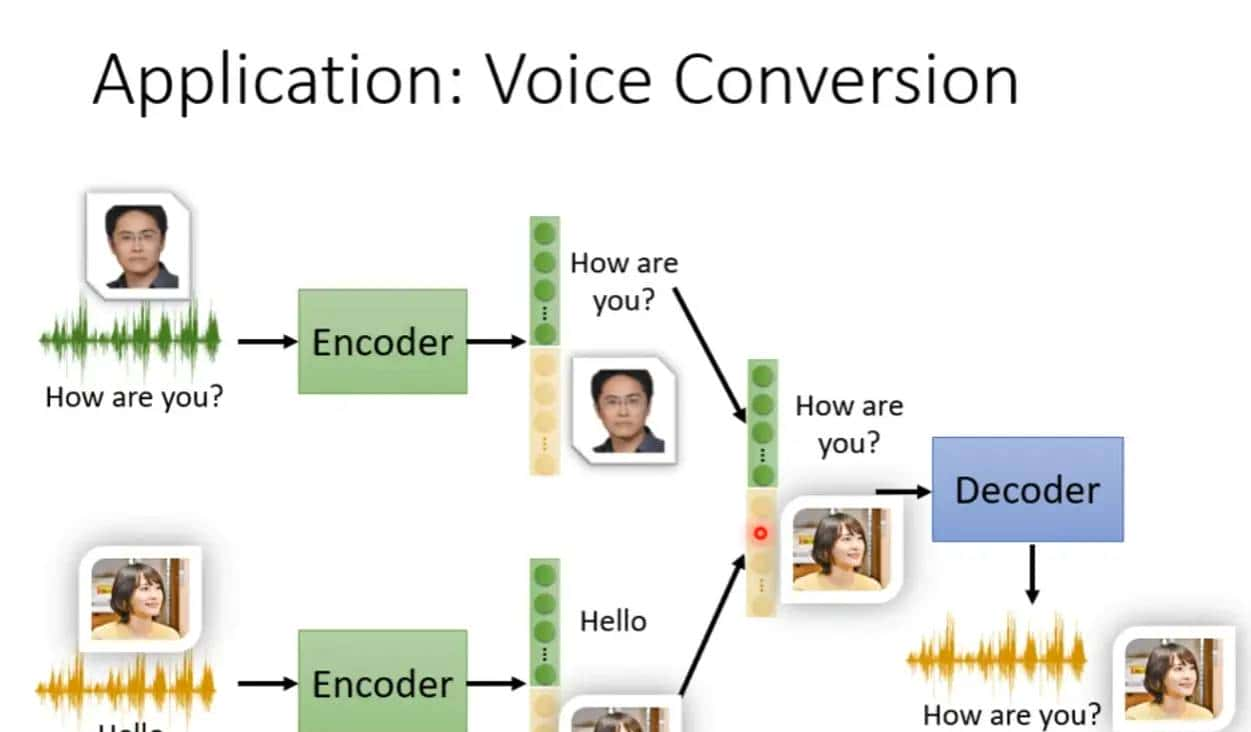
Feature Disentangle应用:声音的转换
找到哪些维度代表某个人说话的内容,哪些维度代表着新桓结衣的这个个体的声音,然后把两个维度合在一起,这样就变成新桓结衣说着原本那个人说话的内容。
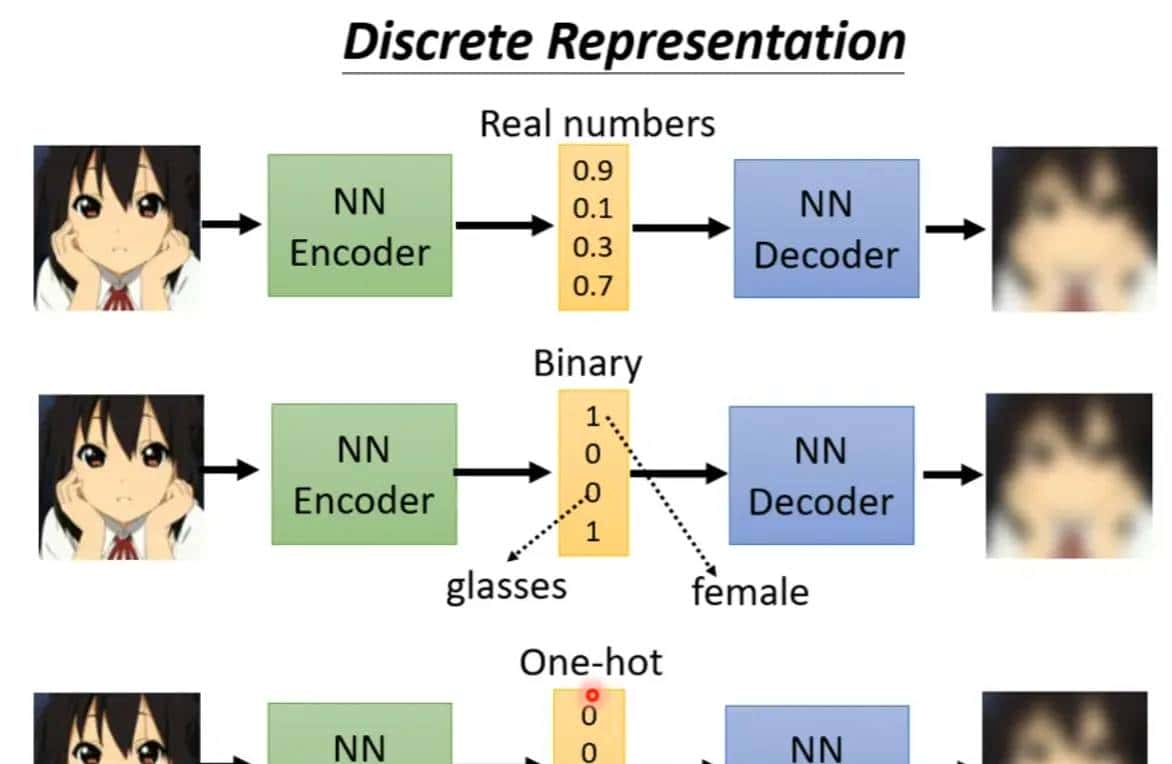
离散潜在表明
学习出向量之后,再将自己学习出的向量和其他的向量(也是学习出来的)计算类似度,(这个过程很类似于self-attention,query和key相乘),然后找出类似度最大的vector,然后把这个vector丢入decoder里面,然后生成图片,这样做实则就是为了让你的表明是有限的,也就是离散的,不是无穷无尽的可能。
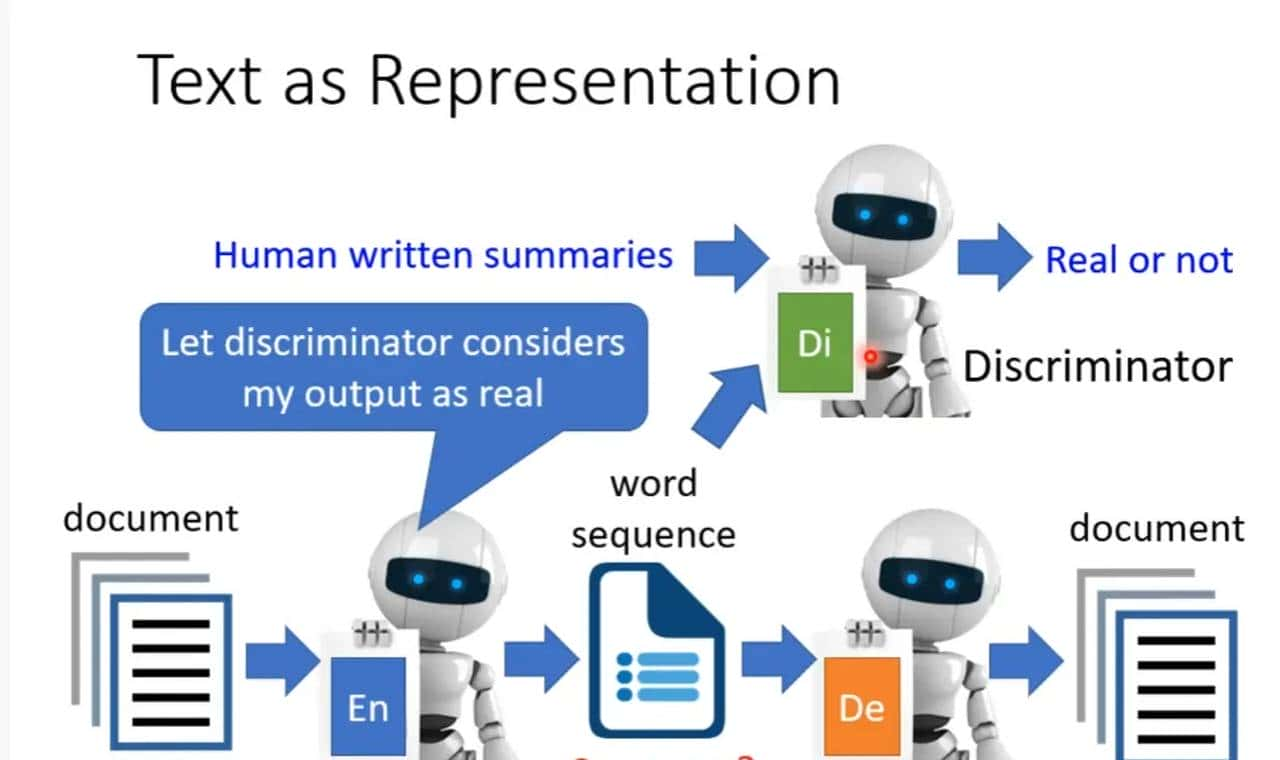
列如文本,就是使用两个seq2seq,一个编码一个解码,但是这样生成的人类不可读,所以还要加一个人类文本进行进一步的纠正
生成器就是吃入一个向量,然后生成一些图片或文字,变分自编码器就是去掉encoder,然后从某些分布之中生成某些向量,然后和decoder拼接起来,VAE就是只要decoder
异常检测Anomaly Detection
检查正常和异常,为什么不直接使用监督学习来检测这样一般的分类问题,由于大多数时候没有正常的资料,这样就没有办法训练而分类器,那么这个时候反而我们使用auto-encoder训练大量的正常资料,获取正常资料的表征,那么遇到异常资料的表征的时候可以分类出异常的结果,而不需要监督的数据
那么怎么进行辨别呢?就是如果训练完之后,这个时候输入一张新的照片,那么如果这张照片符合之前的特征,那么它是能够被还原回来的,如果不符合,那么就不能被还原回来,然后计算输入和输出的差异,如果差异超级大,那么就是异常
其他异常检测的视频
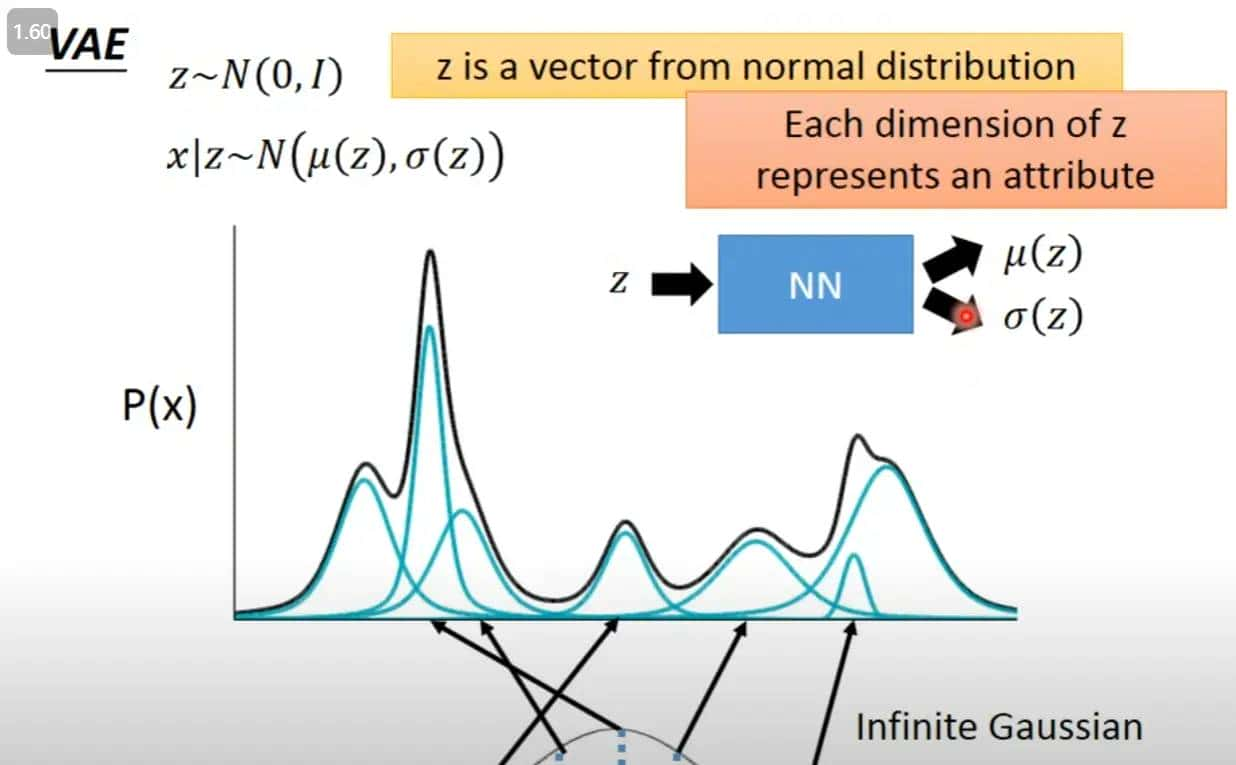
e是从正太分布中学出来的值
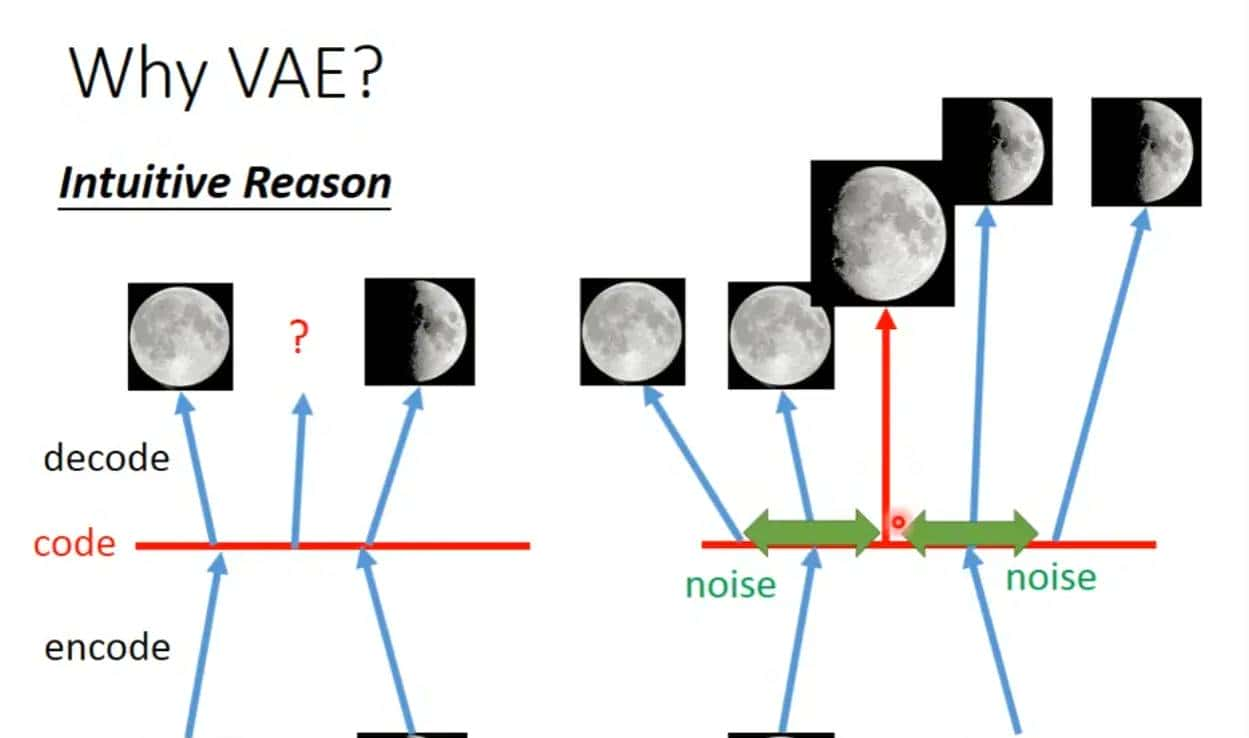
输入弦月和满月, 产生中间的月相

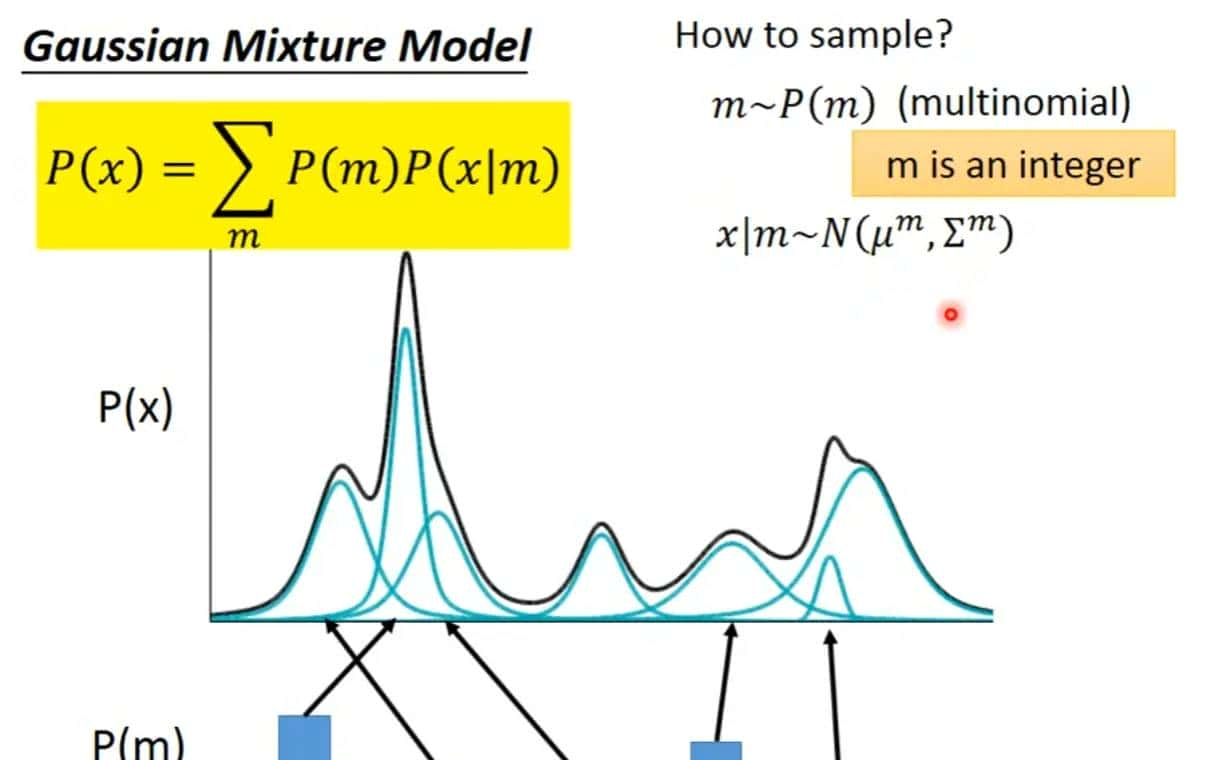
高斯混合分布:从不同的高斯分布之中取值
VAE就是一种高斯混合模型的
后面部分我看视频没有全看懂,就不放了,但是这篇文章的介绍很清晰
变分自编码器(一):原来是这么一回事 – 科学空间|Scientific Spaces (kexue.fm)
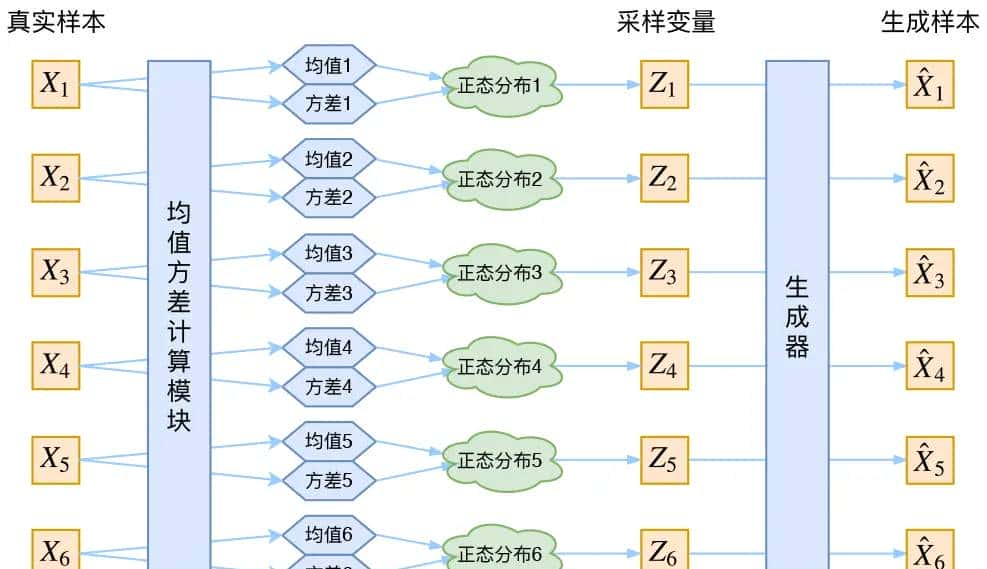
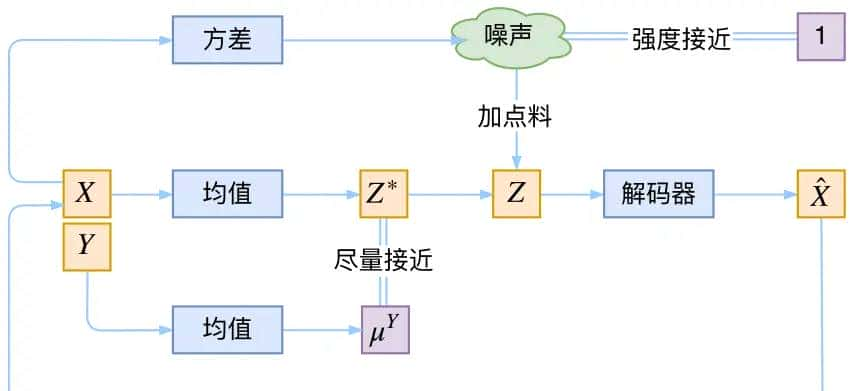
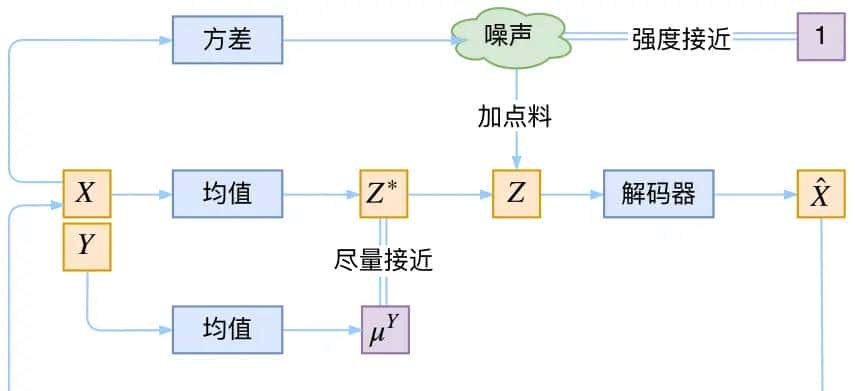
vae的本质结构
VAE的代码实现bojone/vae: a simple vae and cvae from keras (github.com)
GAN
WGAN
互怼的艺术:从零直达WGAN-GP – 科学空间|Scientific Spaces (kexue.fm)
gan/mnist_gangp.py at master · bojone/gan (github.com)
ML Lecture 18: Unsupervised Learning – Deep Generative Model (Part II) – YouTube
变分自编码器(四):一步到位的聚类方案 – 科学空间|Scientific Spaces (kexue.fm)
[bojone/vae: a simple vae and cvae from keras (github.com)](https://github.com/bojone/vae
























暂无评论内容