初中数学阿氏圆问题破题方法归纳总结

知道了阿氏圆的定义，掌握了阿氏圆的性质，这节课我们来学习，阿氏圆的题型有哪些，具体题目中如何构造子母型类似，又是如何解题的。

阿氏圆题型的主要特征：⑴两个定点一个动点，且动点在圆或者圆弧上运动；⑵主要求解形如n.PA±m.PB(m＝n≠1)，即系数不同的两线段的和的最小值或线段差的最大值；⑶还需要满足阿氏圆的半径与阿氏圆的圆心到其中一个定点的比值等于m或n这个系数。第⑶个特征的文字表述不好理解，在具体的题目中，给同学们说清楚。

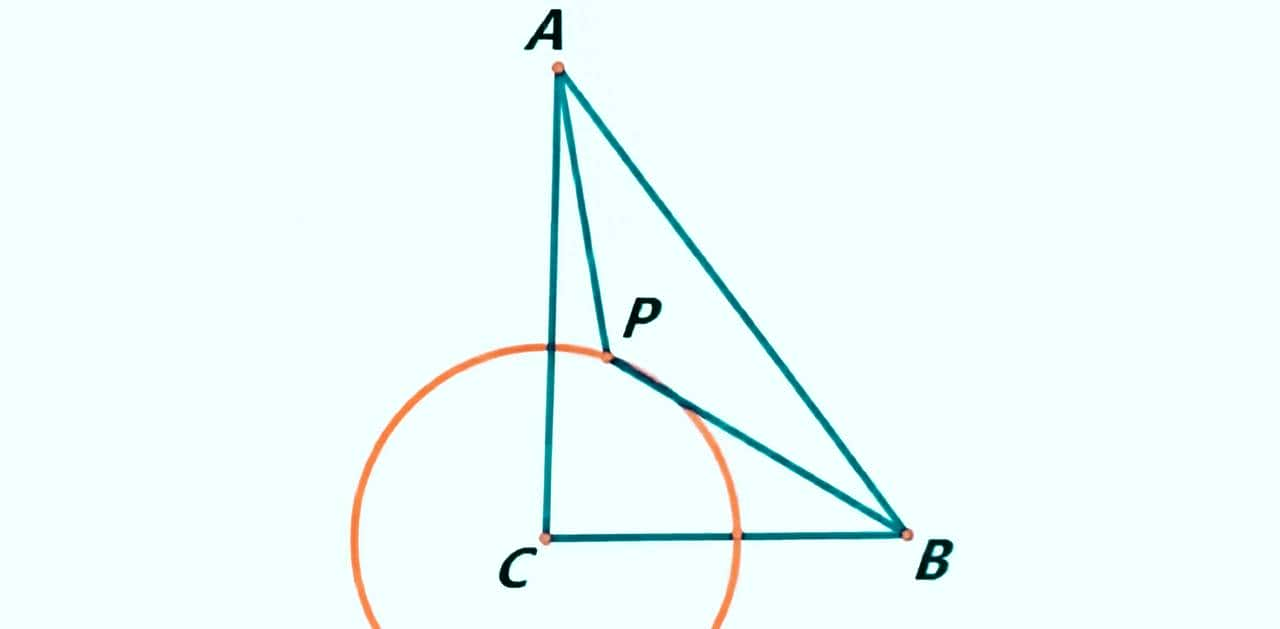
图1

如图1，已知△ABC，∠ACB＝90º，AC＝6，BC＝4，P为⊙C上的动点，⊙C的半径为2。

⑴求PA+PB/2的最小值。

模型判定：由于P的运动轨迹是圆，所以判定这不是胡不归模型。所求线段和的最值出现系数1/2，刚好是半径PC与阿氏圆圆心C到定点B的线段CB的比值，满足阿氏圆最值特征。

线段转化：线段PB的系数不为“1”，我们需要在△PCB中构造出子母型类似，将PB/2转化为一条系数为“1”的线段。

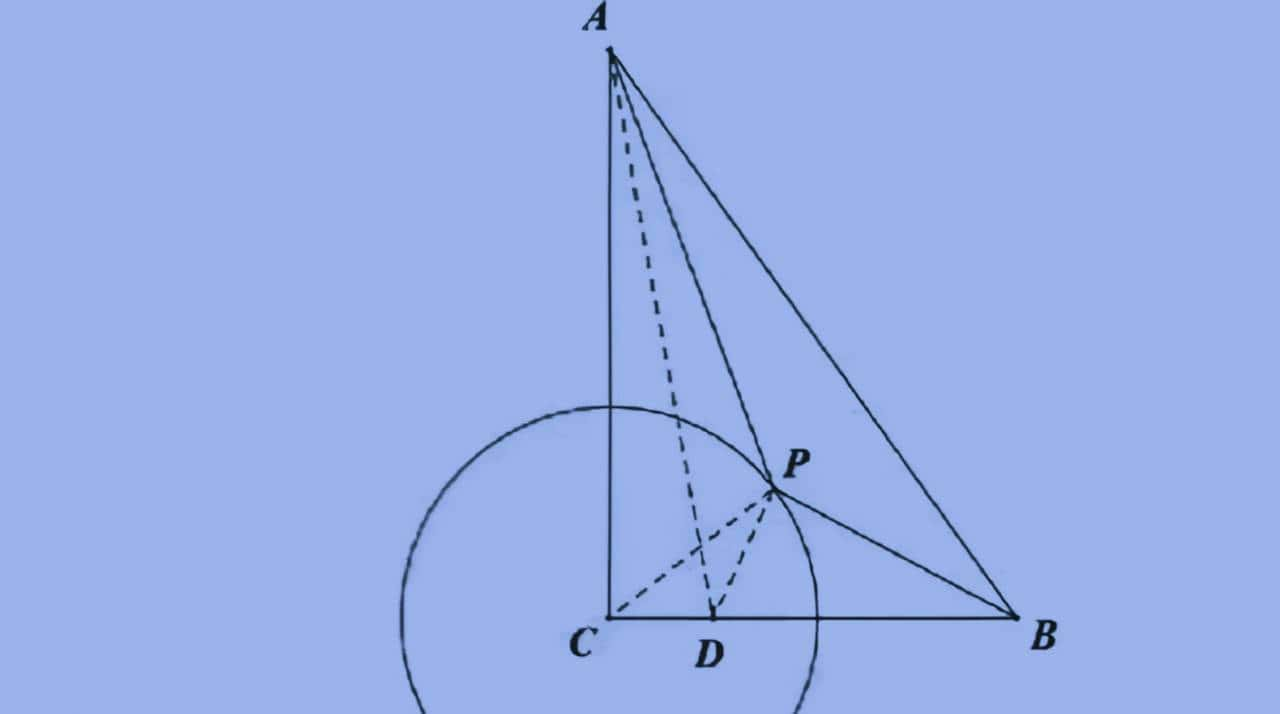
图2

类似三角形构造：如图2，连接PC，以PC为公共边(阿氏圆半径)，以圆心角∠PCB为公共角，在定长线段CB上，确定一个点D，使得PC²＝CD.CB，易得CD＝1，这样就构造出了△PCD∽△BCP。

代入数据求值：原来求PA+PB/2的最小值，就转化为求PA+PD的最小值，显然A，P，D三点共线时取得最小值，大家自己算下。

⑵同样的题目条件，求PB+PA/3。刚好PC：AC＝1/3，就需要将PA/3转化为一条系数为“1”的线段，同样的方法，在△PCA里构造子母型类似。

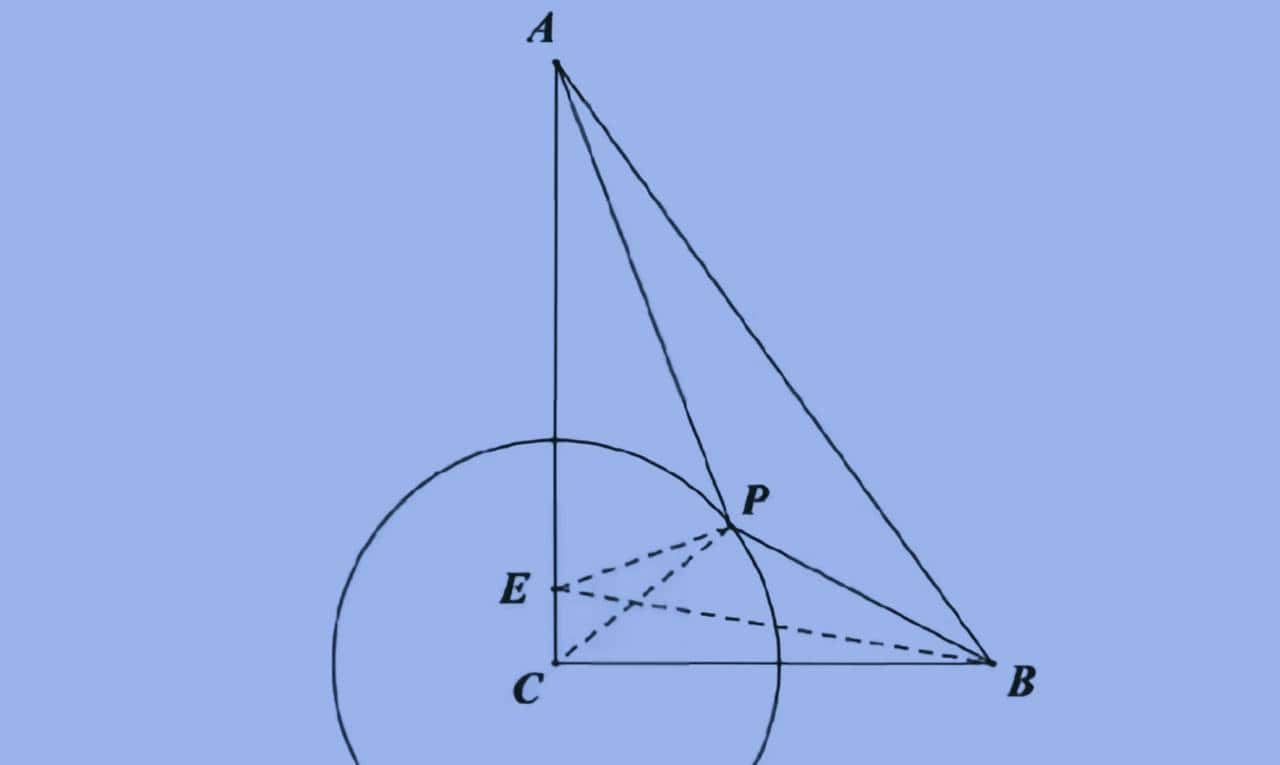
图3

同学们对照图3，按前面所讲的过程，自己试着构造出类似三角形，然后计算出结果。

⑶若求PB+2PA或PA+3PB的最小值。只要把原式分别变形为2(PA+PB/2)和3(PB+PA/3)，构造类似三角形的方法以及最值的原理都是一样的，求得括号里的最值后再乘上括号外对应的系数，就是原式的最小值。

⑷求｜PA-PB/2｜或｜PB-PA/3｜的最大值。构造类似三角形的方法，都是一样的。差的最大值，需要放在一个三角形中，利用两边差小于第三边，当两边差等于第三边时，取得最大值。如求｜PB-PA/3｜的最大值，我们按图3，将PA/3的值转化为线段PE，在△PEB中，PB-PA/3＝PB-PE＜BE，所求PB-PA/3的最大值，就是线段BE的长。

此道例题，属于两定点在阿氏圆外的情形，我们发现，都是在三角形内部构造一个子母型类似，那有没有其它类型的阿氏圆最值问题呢？

欲知后事，请听下回分解！