从零开始的基于FPGA的软件无线电接收机设计——（一）接收模块设计

目录

1 软件无线电基本原理

1.1 软件无线电基本结构

1.2 Nyquist采样定理和带通采样定理

1.3 多速率信号处理技术

1.4 降采样中常用的滤波技术

2 理论计算与总体架构

2.1 接收单元总体架构

2.2 采样方案

2.3 抽取系数

3 信号接收与采样模块的设计与实现

3.1 锁相环模块

3.2 分频模块

---

1 软件无线电基本原理

1.1 软件无线电基本结构

        SDR接收机的物理层可分为基带处理模块和射频前端模块两个子模块，其基本组成包括天线、射频前端、宽带A/D-D/A转换器、通用和专用数字信号处理器，其中理想软件无线电的基本结构如图1所示。

图1 理想软件无线电接收机结构

        软件无线电的基本结构可以分为以下三种：第一种是射频低通采样数字化结构，第二种是射频带通采样数字化结构，第三种是宽带中频带通采样数字化结构。三种结构的示意图分别如图2、图3和图4所示。

图2 射频低通采样数字化结构

图3 射频带通采样数字化结构

图4 宽带中频带通采样数字化结构

        由图可见，宽带中频带通采样数字化结构相较于其他两种结构方案更加复杂，如图4所示，这种结构的优点在于对器件的性能要求最低，适用于宽带信号的接收，其缺点在于结构复杂，可拓展性和灵活性也是最差的，并且它是最不切合理想软件无线电的要求的。射频带通采样数字化结构在A/D转换前使用了带宽相对较窄的电调滤波器，然后根据所需的处理带宽进行带通采样，如图3所示。

        另一方面，射频低通采样数字化结构是最理想的软件无线电结构（如图2），其设计简洁，将模拟电路的数量降至最低。天线接收到的信号经过滤波和放大后，直接由A/D转换器进行采样和数字化处理，从而具备最高的可拓展性和灵活性；然而，理论上这种结构对A/D转换器的性能的要求较高，因此更适合接收信号带宽较窄的应用场合。

        当SDR接收机接收信号的带宽较窄时，A/D器件采样速率的不足可利用带通采样定理以弥补，此时采用射频低通采样数字化结构是较优的选择，并有利于整体设计的灵活性与可拓展性。

---

1.2 Nyquist采样定理和带通采样定理

    Nyquist采样定理，亦称奈奎斯特-香农采样定理，是数字信号处理领域中的一个重要基本定理。哈里·奈奎斯特最初提出了这个定理，随后克劳德·香农对其进行了进一步的发展。根据奈奎斯特定理，要从一个带限信号的样本中准确重建原始信号，采样频率必须至少为信号最高频率的两倍。这一最低采样频率称为奈奎斯特频率。这一原则确保了信号在数字化过程中不丢失任何重要信息，从而实现了高质量的信号重建。

        Nyquist采样又被称为低通采样，它是最基本的采样形式，其基本内容为：设有一个低通带限在(0,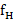 )内的连续信号x(t)，如果以不小于 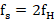的采样速率对x(t)进行等间隔采样，则x(t)可以被所得到的采样值完全确定。

        当 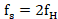 ，刚好可以无失真地恢复原信号；当 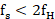时，会发生频谱混叠现象，如图5所示。

图5 原始频谱与采样后频谱

        但假如系统中最高频率很高，使用低通采样方式对信号进行采样所需要的采样频率将会非常高，这对器件的性能提出了相当高的要求；再者，在信道中传输的信号基本都经过调制，属于带通信号，假如用低通采样定理进行采样，采样后的频谱间隔很远，这造成了极大的浪费，如图6所示。

图6 带通信号的奈奎斯特采样

        为了解决这些问题，需要运用带通采样定理。带通采样定理是奈奎斯特采样定理的一个扩展，适用于那些频率成分不是从零开始的信号。对于带通信号，其频率范围可能从某个非零的最低频率到最高频率。我们可以使用低于传统奈奎斯特频率的采样频率对其进行采样，而不会导致信号混叠。

依照带通采样定理，如果信号的频带宽度是 ，那么最小采样速率

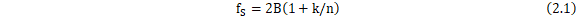
其中k为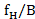  的小数部分，n为  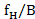 的整数部分。下面进行简单推导。

图7 带通采样定理

如图7所示，对于这样一个频带位于 (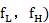 之间的信号，其信号带宽为B，当以  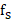的采样速率对原信号进行采样时，为了避免频谱混叠，采样速率 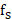应当要满足以下关系：

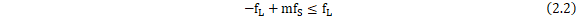
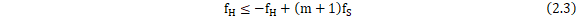
整理得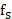， 的取值范围为：

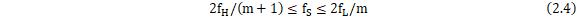
其中，m为非负整数，其含义是m次频移。显然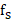， 存在的条件为：

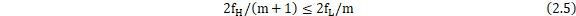
化简可得：

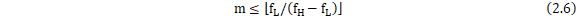
        带通采样定理允许在更低的采样频率下进行采样，减少了硬件对高速A/D转换器的需求，从而降低了成本和复杂度。同时，带通采样定理提供了多个符合条件的采样频率，使设计者可以根据具体应用需求和硬件限制选择最合适的采样率。

        带通采样定理在软件无线电中的应用非常关键，通过适当的采样率选择，SDR系统可以有效地调整和选择想要接收的信号频带，实现高效的频率转换和信号处理；SDR系统还可以通过带通采样技术接收和处理宽频带信号，如直接采样整个无线电频谱的部分频段，然后通过软件选择性地分析特定的信号。

---

1.3 多速率信号处理技术

         根据对软件无线电的要求，越高的信号采样速率越能确保信号不失真。此外，提高采样速率会增加瞬时采样带宽，从而增强对不同信号的适应能力。相反，对于高频射频信号，过低的采样频率会降低采样量化的信噪比。

        然而，采样速率的提高会导致数据流速率增加，可能导致后续信号处理速度不足。此外，特别是对于本文所设计的这类接收机而言，后续还涉及解调、信号识别等多种复杂处理，其计算量大、数据吞吐量高，因此对A/D转换后的数据流进行降速处理是很有必要的。多速率信号处理技术提供了实现这种降速处理的理论基础，其中抽取和内插是理论的核心。

        整倍数抽取是指把原始采样序列x(n)每隔D-1个数据取一次，以形成一个新序列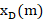 ，即

     

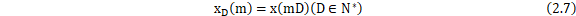
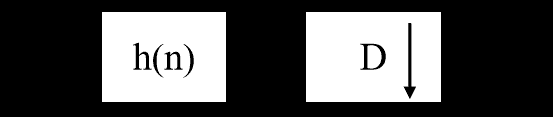
图8 抽取器

        假设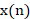 是对模拟信号 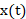以采样频率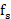 采样得到的信号，其频谱为 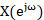，那么在频率区间 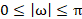（对应的模拟区间是 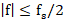）是非零的。按整数因子 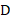对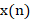 进行抽取，如果简单地对 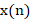每隔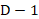 个样值抽取1个，使采样频率降低为 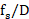，那么可能产生严重的频谱混叠，如图9。

图9 抽取前后（D=2）的频谱结构（混叠）

图10 进行抗混叠滤波后的抽取的频谱结构

所以当信号最高频率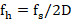 时，才能保证频谱不混叠，为了让所有抽取信号刚好满足这个条件，需要进行抗混叠滤波，如图10。

理想情况下，抗混叠滤波器的频率响应为

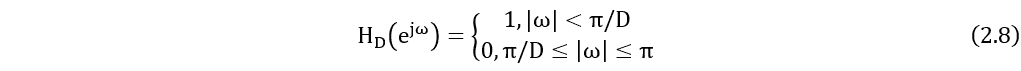
实际的滤波器不可能如此陡峭，所以我们设计的滤波器只要满足通带截止频率是需要保留的最高频率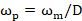 ，阻带截止频率是 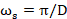，即可完成抗混叠滤波功能，如图11。

图11 非理想的抗混叠滤波器

---

1.4 降采样中常用的滤波技术

（1）FIR滤波器

        由上一节中可知，为了抑制降采样过程中可能引起的频谱泄漏和混叠等现象，需要在抽取前对信号进行滤波处理，这是采样率变换（降采样）的关键问题。

        数字滤波器可以以两种形式实现：有限冲激响应滤波器 (FIR) 和无限冲激响应滤波器 (IIR)。在软件无线电系统设计中，FIR滤波器比IIR滤波器具有明显的优势，如线性相位和更高的稳定性。此外，FIR滤波器的设计方法丰富且成熟，因此在软件无线电系统中，通常优先选择FIR滤波器进行实现。

        FIR滤波器的基本结构由多个延迟器和一组可调的加权系数组成。延迟器用于保存先前的输入信号样本，而加权系数决定了每个延迟器输出的权重。输入信号通过延迟器后，与相应的加权系数相乘，并将结果相加，生成最终的输出信号。这种结构使得FIR滤波器的输出只依赖于有限数量的过去输入信号样本，而不依赖于无限的过去样本。

        FIR滤波器的工作原理可以用数学形式表示为

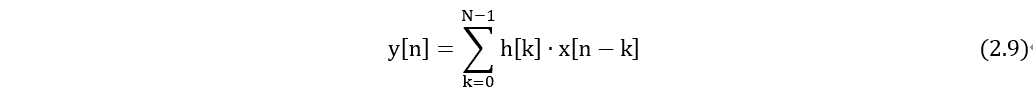
        其中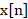， 是输入信号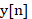， 是输出信号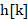， 是滤波器的系数，N是滤波器的长度。这个公式说明了输出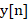信号 是输入信号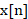 与滤波器系数 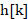的线性组合。

（2）CIC滤波器

        在软件无线电领域，积分梳状滤波器（CIC）被广泛应用，主要用于降低抽取率、滤除高频噪声和不必要的信号成分。CIC滤波器之所以广泛应用，得益于其优异的特性：即结构简单、性能高效以及无需乘法器。由于这些优点，CIC滤波器非常适合应用在基于FPGA的SDR接收机中，可以大大节省运算资源，保证系统优异的实时性。

        CIC滤波器由积分器和梳妆滤波器构成，其实质上是递归求和滤波器。下面进行详细介绍。

        积分器（如图12）是一种用于对信号进行积分操作的电路或数字滤波器。在时域上，积分器的作用类似于对信号进行累积，进而输出信号。在离散时间中，积分器可以通过差分方程来表示：

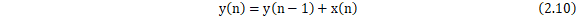
        其中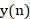， 是输出信号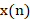， 是输入信号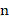， 是离散时间的样本索引。这表示输出信号是输入信号的当前样本值与前一时刻输出信号值的累积。用z变换推导，积分器的系统响应（传递函数）应为：

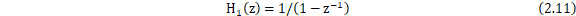
图12 积分器

        梳状滤波器（参见图13）是一种常见的滤波器结构。它在频域中表现为周期性的谱线，形状类似梳子，因此得名。梳状滤波器主要用于处理信号中的周期性成分，能够增强或抑制特定频率的信号。其方程具有如下形式：

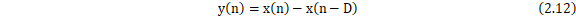
        其中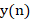，  是滤波器的输出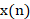， 是输入信号的当前样本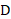， 是延迟因子，一般等于抽取或内插的倍数。梳状滤波器的系统响应为：

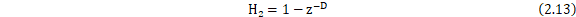
图13 梳状滤波器

        CIC滤波器是将积分器与梳状滤波器进行级联，如图14所示。因此，CIC滤波器的系统响应为：

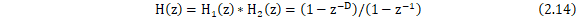
        易得，CIC滤波器的频率响应为：

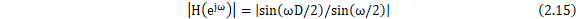
图14 二级CIC降采样滤波器

        如图15，可以看到CIC滤波器的频谱类似梳齿，并且梳齿在逐渐衰减。然而，多级CIC的通带较窄，对于这一缺点，有两种解决方法：

图15 CIC滤波器频谱（D=40）

        一种方案是，使用CIC滤波器进行初步降采样，然后级联半带滤波器或FIR滤波器进行进一步处理。另一种处理方案是使用补偿滤波器对通带内的频率响应进行补偿，补偿滤波器的设计方法是创建一个在通带内频率响应为CIC滤波器频率响应倒数的滤波器，将这两个滤波器级联后，能够实现通带内频率响应的平稳。

        在本设计中，采用第一种方案。

---

2 理论计算与总体架构

2.1 接收单元总体架构

        计划设计的接收机接收频带位于 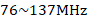 之间，带宽B为61MHz；对于硬件部分，系统配备的A/D转换器最大采样频率为100MHz，在系统末端用于信号输出的DAC采样频率为48kSPS。        

        因此，必须采用小于100MHz的采样频率完成无失真的信号采样，并且要在输出前完成信号采样率变换，将信号速率降到48kSPS。

        根据前几节的理论研究，可以构建出接收机的降采样单元的结构，如图16所示。下面将介绍设计思路和参数计算。

图16 降采样模块设计

---

2.2 采样方案

        首先考虑信号采样部分，如果对信号直接进行采样，需要遵从奈奎斯特采样定理，需要的采样频率为：

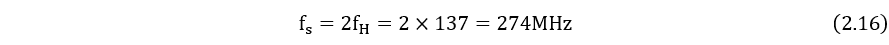
        这显然不可能实现，因此，将待采样信号分为两路，即  与，分别记为 S1 与 S2，频率范围。

        对于S1,根据式 (2.5) 和式 (2.6)，运用带通采样定理：

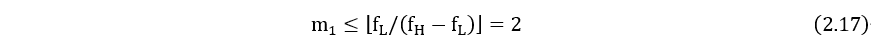
        故 可取 1 和 2。当 ，采样频率  可取 ，无法实现，故舍弃；当 ，采样频率可取 。

        对于S2，根据式 (2.5) 和式 (2.6)，运用带通采样定理：

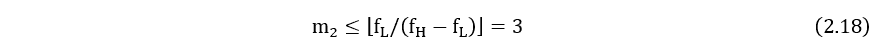
        故  可取 1、2 和 3。当 ，采样频率  可取 ，舍弃；当 ，采样频率  可取 ；当 ，采样频率  可取 。

        最终采样频率的可选范围如表1所示。

表1 采样频率可选范围

信号频率范围（MHz）	m取值	fs（MHz）
76~106.5	2	71~76
106.5~137	2	91.33~106.5
106.5~137	3	68.5~71

        参数m意味着m次频移，其数值的选择会影响后续滤波器的设计；并且，对于FPGA器件而言，不同的频率一般是使用锁相环（PLL）IP核分频得到，因此若选取的频率太过于接近，会导致难以通过分频得到且分频精度下降的问题。综合以上因素，对于S1和S2两组信号，都采用2次频移，即m=2，相应的采样频率也从对应的可选范围来选取。

---

2.3 抽取系数

为了进一步确定采样频率，还需要确定整个系统的下变频倍数M，并为CIC滤波器和FIR滤波器分配抽取系数，参数M与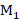 、 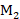的关系如式（2.19）所示。

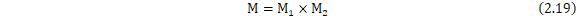
由于解调过程需要的频带约为400kHz，由式（2.20）可知，在DA转换之前，FIR滤波器应当对信号实现8倍的抽取，因此可以先确定 。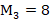

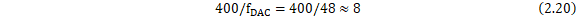
接下来，以S1信号的接收为例。根据图2-16的结构，列出式（2.21）。

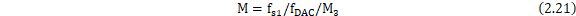
可以计算出M的取值范围约为185~197，由于M需要拆分为两个正整数之积，故M必须为合数，不妨取M为192，则ADC的采样频率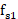 为：

 而FIR滤波器的采样频率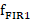 为：

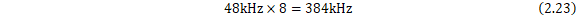
由此，可取滤波器的截频为192kHz，即采样频率的一半。

在二级抽取系统中，可通过理论计算算出抽取系数的最优值，如式（2.24）和式（2.25）。

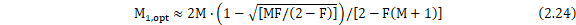
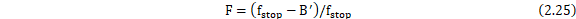
其中，F为滤波器的平坦通带带宽与其截频的比值。取过渡带带宽为2kHz，可计算得：

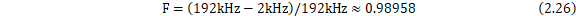
       将数值代入式（2.24）计算可得：

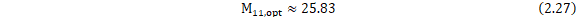
              由于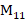 必须能被M整除，故应当取 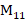为24，根据式（2.19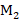）， 应当为8。由此，已经可以确定适用于S1信号的降采样模块的所有参数，如表2所示。

表2 S1信号（76~106.5MHz）降采样模块参数

参数名称	取值
fs1	73.728MHz
fCIC	3.072MHz
fFIR1	384kHz
fFIR2	48kHz
M11	24
M2	8

接下来，考虑S2信号的接收，显然采样频率会发生变化，随之需要变化的是系统的下变频倍数M，事实上，只要改动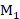 或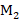 中的一个即可。考虑到CIC滤波器的抽取系数改动起来更为简便，因此保持 不变，改动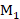 ，由式（2.28）：

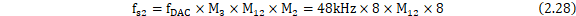
       由于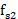 的取值范围是91.33~106.5MHz，故 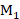只能取30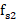， 为92.16MHz。由此，已经可以确定适用于S2信号的降采样模块的所有参数，如表3所示。

表3 S2信号（106.5~137MHz）降采样模块参数

参数名称	取值
fs2	92.16MHz
fCIC	3.072MHz
fFIR1	384kHz
fFIR2	48kHz
M12	30
M2	8

---

3 信号接收与采样模块的设计与实现

3.1 锁相环模块

        本系统采用的FPGA核心板上的系统时钟为12MHz，为了实现不同速率时钟信号的生成，可以使用Quartus Prime中自带的IP核ALTPLL对系统时钟进行频率合成，即生成比输入时钟频率高的时钟信号。

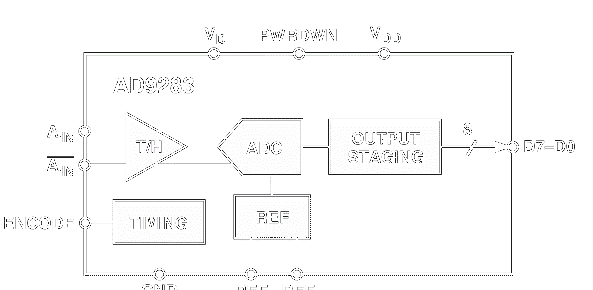
图3-5 芯片AD9283BRS-100

        根据上节可知，本系统需要频率分别为73.728MHz和92.16MHz的两个采样时钟，用以驱动ADC芯片AD9283BRS-100（如图3-5）。此外，在nco生成正余弦信号之后需要与原信号分别进行混频，此时需要更高速率的时钟，应当保证在下一次采样前完成本次采样信号的混频，因此还需要两倍于两个采样时钟的147.456MHz和184.32MHz时钟信号。最后，在系统核心的信号处理之外，还存在按键检测、按键控制逻辑和数据显示等部分的功能模块，倘若这些部分也用高至几兆赫兹的时钟频率来处理，不仅对于系统资源和功耗是一种极大浪费，还容易导致按键误触等问题，因此还需要使用PLL分频出一个尽可能小一些的时钟信号。综上，系统中所有时钟如表3-2所示，包括一个系统时钟、一个使用分频模块产生的时钟和五个使用PLL生成的时钟。

表3-2 程序内时钟

时钟名称	理论频率（MHz）	实际频率（MHz）	功能
CLK	12	12	系统时钟
clk_0	73.728	73.8	针对S1（76~106.5MHz）信号
clk_0_2x	147.456	147.6	用于S1信号输入时的混频模块
clk_mid	1.5	1.5	分频后产生clk_1用于按键、显示等模块
clk_2	92.16	92.25	针对S2（106.5~137MHz）信号
clk_2_2x	184.32	184.5	用于S2信号输入时的混频模块
clk_1	0.005	0.005	用于按键、显示等模块

图3-6 IP核选择

        使用PLL IP核生成所需时钟的配置过程如下：首先，打开Quartus Prime的IP核列表，在表中找到ALTPLL，如图3-6所示。接下来，对该模块进行命名以及设置储存路径，在IP核弹出页面的“Parameter Settings”页面配置好系统的时钟频率，即12MHz。然后，在“Output Clocks”模块对待输出时钟进行设置，五个可选项全部启用，并设置好所需频率，如图3-7所示。

图3-7 PLL参数配置

        值得一提的是，PLL模块并不能产生任意的无偏差的时钟，所生成的结果不仅会有所误差，并且会互相影响。当设置clk_c0合成高至几十兆赫兹的时钟后，可以生成的其他时钟最少只能低至1.5MHz。PLL模块符号如图3-8所示。

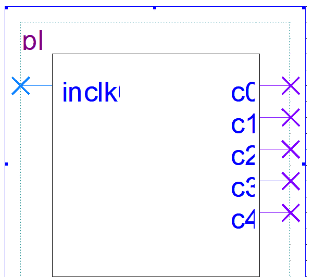
图3-8 PLL模块符号

---

3.2 分频模块

采用PLL可以生成的最低时钟频率为1.5MHz，这个频率对于按键及显示模块来说还是太高了，因此需要编写程序对clk_mid进行分频。分频模块的接口说明如表3-3所示，模块符号如图3-9所示。

对于任意分频计数器，可分为偶数分频和奇数分频两种情况进行讨论。

偶数分频较为简单，例如实现N倍偶数分频时，通过计数器计数，当计数器从0计数到N/2-1时，输出时钟翻转，依次循环。

奇数分频较复杂。若在计数到一半时翻转输出时钟，将无法得到占空比为50%的时钟。因此，需要在上升沿和下降沿进行模N计数。当计数到某一值时，输出时钟翻转，经过（N-1）/2后再次翻转，得到占空比不为50%的奇数N分频时钟。通过对两个占空比不为50%的N分频时钟进行逻辑运算，即可获得占空比为50%的奇数N分频时钟。

对于分频系数，不妨选择300，因此有：

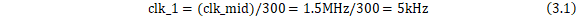
得到的5kHz时钟适用于按键检测和显示模块。

表3-3 divide模块接口说明

接口名称	输入/输出	信号说明
clk	输入	待分频的输入时钟
rst_n	输入	复位信号
num	输入	分频系数
clkout	输出	分频后的时钟输出

图3-9 divide模块符号